跳轉到主要內容
部落格

使用半結構化 (2:4) 稀疏性加速神經網路訓練

作者： 2024 年 6 月 20 日2024 年 11 月 13 日暫無評論

在過去的一年裡，我們已將半結構化 (2:4) 稀疏性支援新增到 PyTorch 中。只需幾行程式碼，我們就能在 Segment-Anything 上將密集矩陣乘法替換為稀疏矩陣乘法，從而實現 10% 的端到端推理速度提升。

然而，矩陣乘法並非神經網路推理獨有，它們在訓練期間也會發生。透過擴充套件我們早期用於加速推理的核心原語，我們還能夠加速模型訓練。我們編寫了一個替換的 nn.Linear 層 SemiSparseLinear，它能夠在 NVIDIA A100 上實現 ViT-L 的 MLP 塊中線性層的前向 + 反向傳遞 1.3 倍的 加速。

端到端來看，DINOv2 ViT-L 訓練的實際執行時間減少了 6%，且開箱即用的準確度幾乎沒有下降（ImageNet top-1 準確度為 82.8 vs 82.7）。

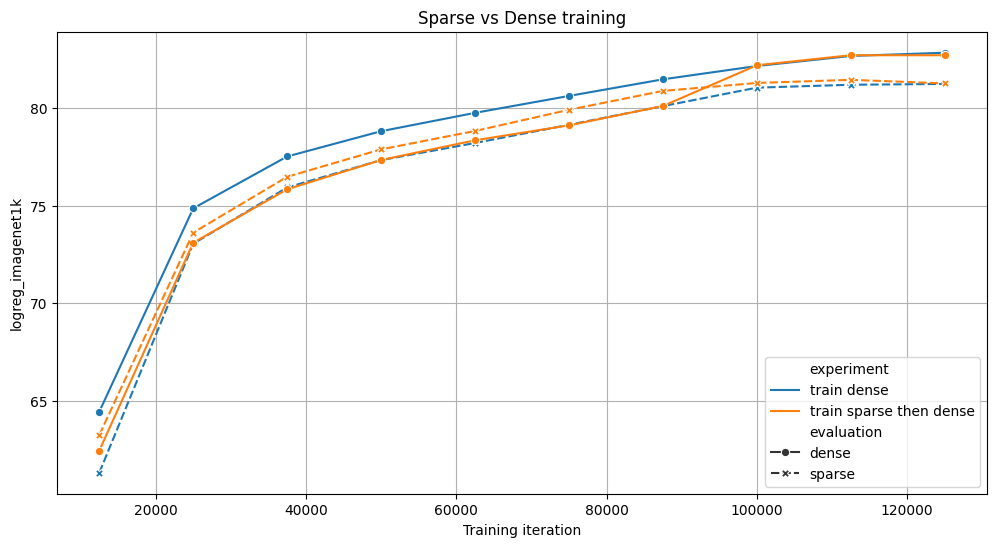
2 strategies for training a ViT model

我們比較了在 4 個 NVIDIA A100 上訓練 ViT 模型 125k 次迭代的兩種策略：完全密集（藍色）或 70% 的訓練是稀疏的，然後是密集（橙色）。兩者在基準測試中都取得了相似的結果，但稀疏變體訓練速度快了 6%。對於這兩個實驗，我們評估了有和沒有稀疏性的中間檢查點。

據我們所知，**這是第一個加速稀疏訓練的開源實現**，我們很高興能在 torchao 中提供使用者 API。你只需幾行程式碼即可嘗試加速你自己的訓練執行。

# Requires torchao and pytorch nightlies and CUDA compute capability 8.0+
import torch
from torchao.sparsity.training import (
    SemiSparseLinear,
    swap_linear_with_semi_sparse_linear,
)

model = torch.nn.Sequential(torch.nn.Linear(1024, 4096)).cuda().half()

# Specify the fully-qualified-name of the nn.Linear modules you want to swap
sparse_config = {
    "seq.0": SemiSparseLinear
}

# Swap nn.Linear with SemiSparseLinear, you can run your normal training loop after this step
swap_linear_with_semi_sparse_linear(model, sparse_config)

它是如何工作的？

稀疏性背後的總體思想很簡單：跳過涉及零值張量元素的計算，以加速矩陣乘法。然而，僅僅將權重設定為零是不夠的，因為密集張量仍然包含這些修剪過的元素，並且密集矩陣乘法核將繼續處理它們，從而產生相同的延遲和記憶體開銷。為了實現實際的效能增益，我們需要用智慧地繞過涉及修剪過的元素的計算的稀疏核來替換密集核。

這些核心作用於稀疏矩陣，這些矩陣刪除修剪過的元素並以壓縮格式儲存指定的元素。有許多不同的稀疏格式，但我們特別感興趣的是**半結構化稀疏性**，也稱為**2:4 結構化稀疏性**或**細粒度結構化稀疏性**，更一般地稱為**N:M 結構化稀疏性**。

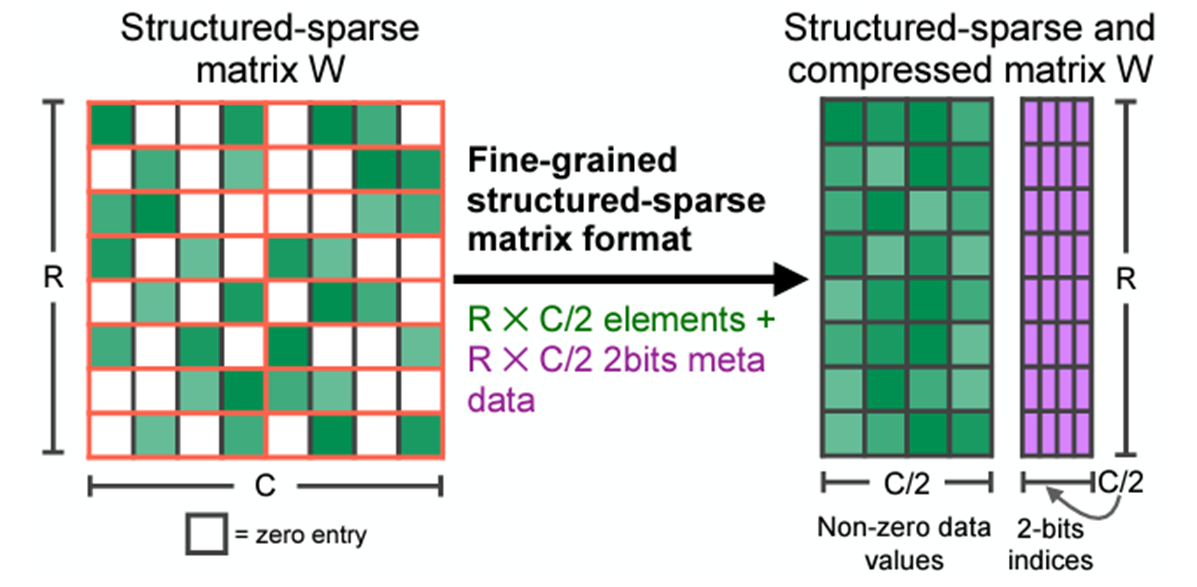
2:4 sparse compressed representation

2:4 稀疏壓縮表示。原始 來源

2:4 稀疏矩陣是一個矩陣，其中每 4 個元素中最多有 2 個非零元素，如上圖所示。半結構化稀疏性之所以具有吸引力，是因為它在效能和準確性之間找到了一個完美的平衡點。

  1. 自 Ampere 架構以來的 NVIDIA GPU 為這種格式提供硬體加速和庫支援 (cuSPARSELt)，矩陣乘法速度最高可達 1.6 倍。
  2. 修剪模型以適應這種稀疏模式，其準確性下降不如其他模式那樣嚴重。NVIDIA 的 白皮書 顯示，修剪然後重新訓練能夠恢復大多數視覺模型的準確性。
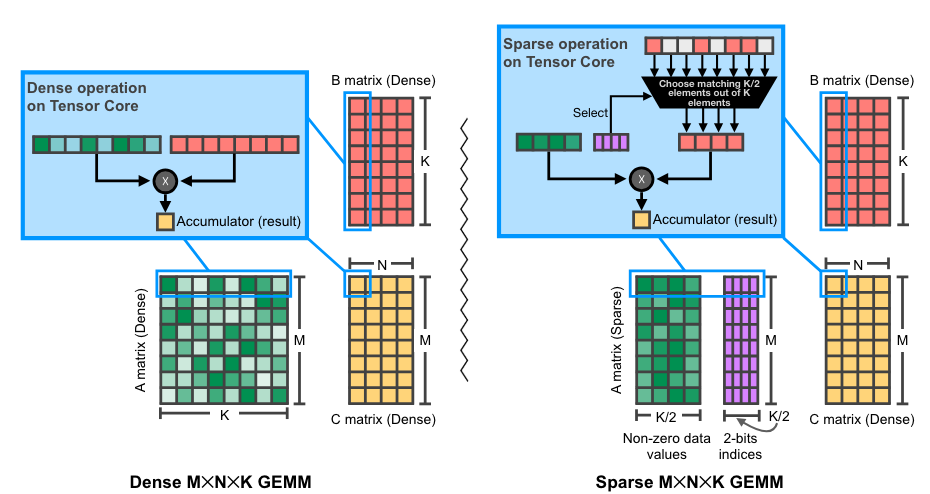
Illustration of 2:4 (sparse) matrix multiplication on NVIDIA GPUs

NVIDIA GPU 上 2:4 (稀疏) 矩陣乘法的圖示。原始 來源

使用半結構化稀疏性加速推理很簡單。由於我們的權重在推理過程中是固定的，我們可以提前（離線）修剪和壓縮權重，並存儲壓縮的稀疏表示而不是密集張量。

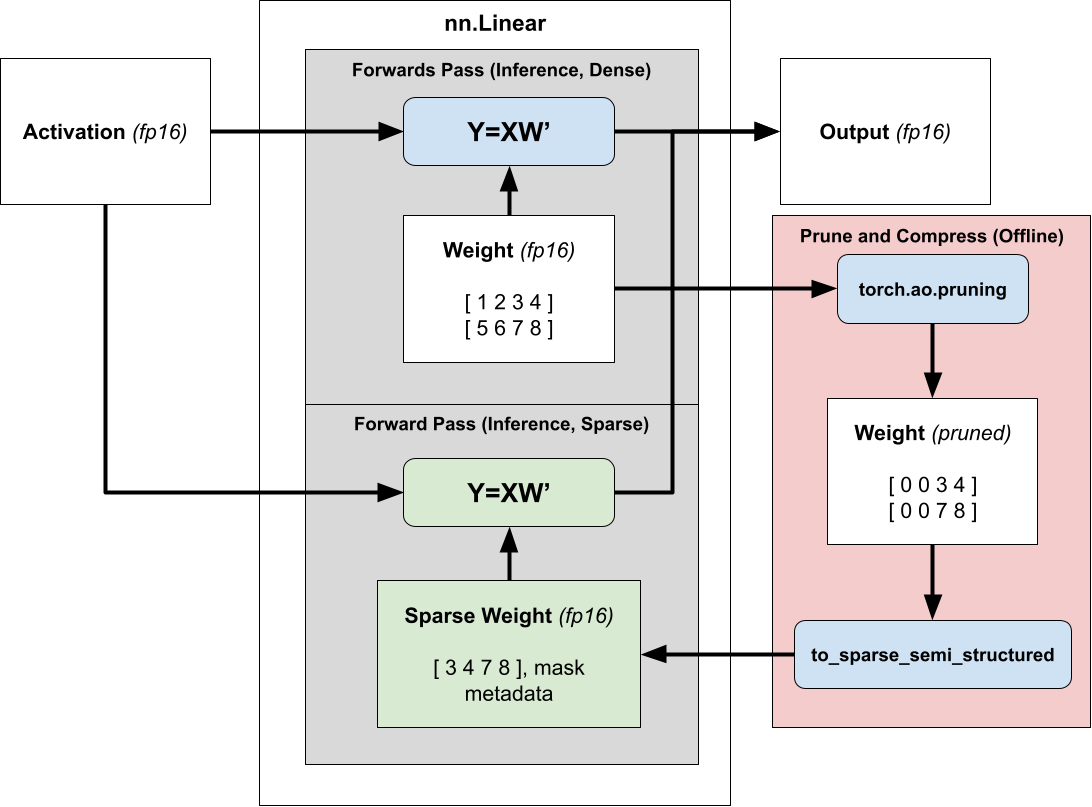
flow chart

然後，我們不再排程密集矩陣乘法，而是排程稀疏矩陣乘法，傳入壓縮的稀疏權重而不是正常的密集權重。有關使用 2:4 稀疏性加速模型推理的更多資訊，請參閱我們的 教程。

將稀疏推理加速擴充套件到訓練

為了利用稀疏性來減少模型的訓練時間，我們需要考慮何時計算掩碼，因為一旦我們儲存了壓縮表示，掩碼就會固定。

用應用於現有訓練好的密集模型的固定掩碼進行訓練（也稱為**修剪**）不會降低準確性，但這需要兩次訓練執行——一次用於獲取密集模型，另一次用於使其稀疏，這樣並不能提供加速。

相反，我們希望從頭開始訓練稀疏模型（**動態稀疏訓練**），但從頭開始使用固定掩碼進行訓練會導致評估顯著下降，因為稀疏性掩碼將在初始化時選擇，此時模型權重本質上是隨機的。

為了在從頭開始訓練時保持模型的準確性，我們在執行時修剪和壓縮權重，以便我們可以在訓練過程的每個步驟計算最優掩碼。

從概念上講，你可以將我們的方法視為一種近似矩陣乘法技術，我們 `prune_and_compress` 並分派到 `sparse_GEMM` 所需的時間少於 `dense_GEMM` 呼叫所需的時間。這很困難，因為原生修剪和壓縮函式太慢，無法顯示出加速效果。

鑑於我們 ViT-L 訓練矩陣乘法的形狀（13008x4096x1024），我們測量了密集 GEMM 和稀疏 GEMM 的執行時間分別為 538us 和 387us。換句話說，權重矩陣的修剪和壓縮步驟必須在小於 538-387=151us 的時間內執行才能獲得任何效率增益。不幸的是，cuSPARSELt 中提供的壓縮核心已經需要 380us（甚至沒有考慮修剪步驟！）。

考慮到 NVIDIA A100 的最大記憶體 IO（2TB/s），並且考慮到修剪和壓縮核心會受記憶體限制，我們理論上可以在 4us 內（8MB / 2TB/s！）修剪和壓縮我們的權重（4096x1024x2 位元組=8MB）！事實上，我們能夠編寫一個核心，將矩陣修剪並壓縮為 2:4 稀疏格式，並在 36 us 內執行（比 cuSPARSELt 中的壓縮核心快 10 倍），使整個 GEMM（包括稀疏化）更快。我們的核心已在 PyTorch 中 可用。

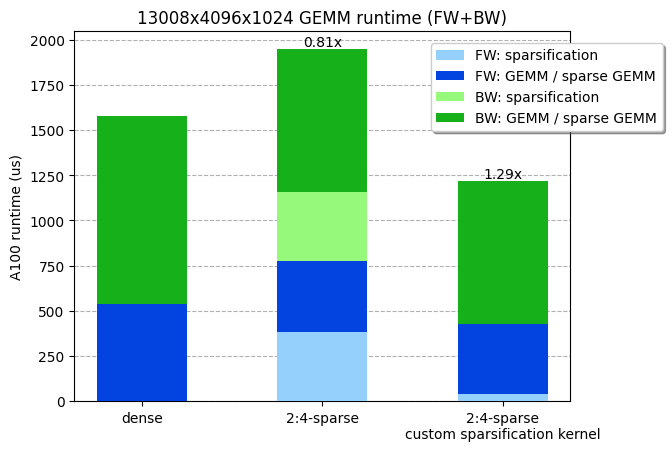
Our custom sparsification kernel

我們定製的稀疏化核心，包括修剪 + 壓縮，線上性層前向 + 反向傳遞中快了約 30%。基準測試在 NVIDIA A100-80GB GPU 上執行。

編寫高效能執行時稀疏化核心

為了實現高效能執行時稀疏化核心，我們面臨著多項挑戰，我們將在下面探討。

1) 處理反向傳播

對於反向傳播，我們需要計算 dL/dX 和 dL/dW 以進行梯度更新和後續層，這意味著我們需要分別計算 xWT 和 xTW。

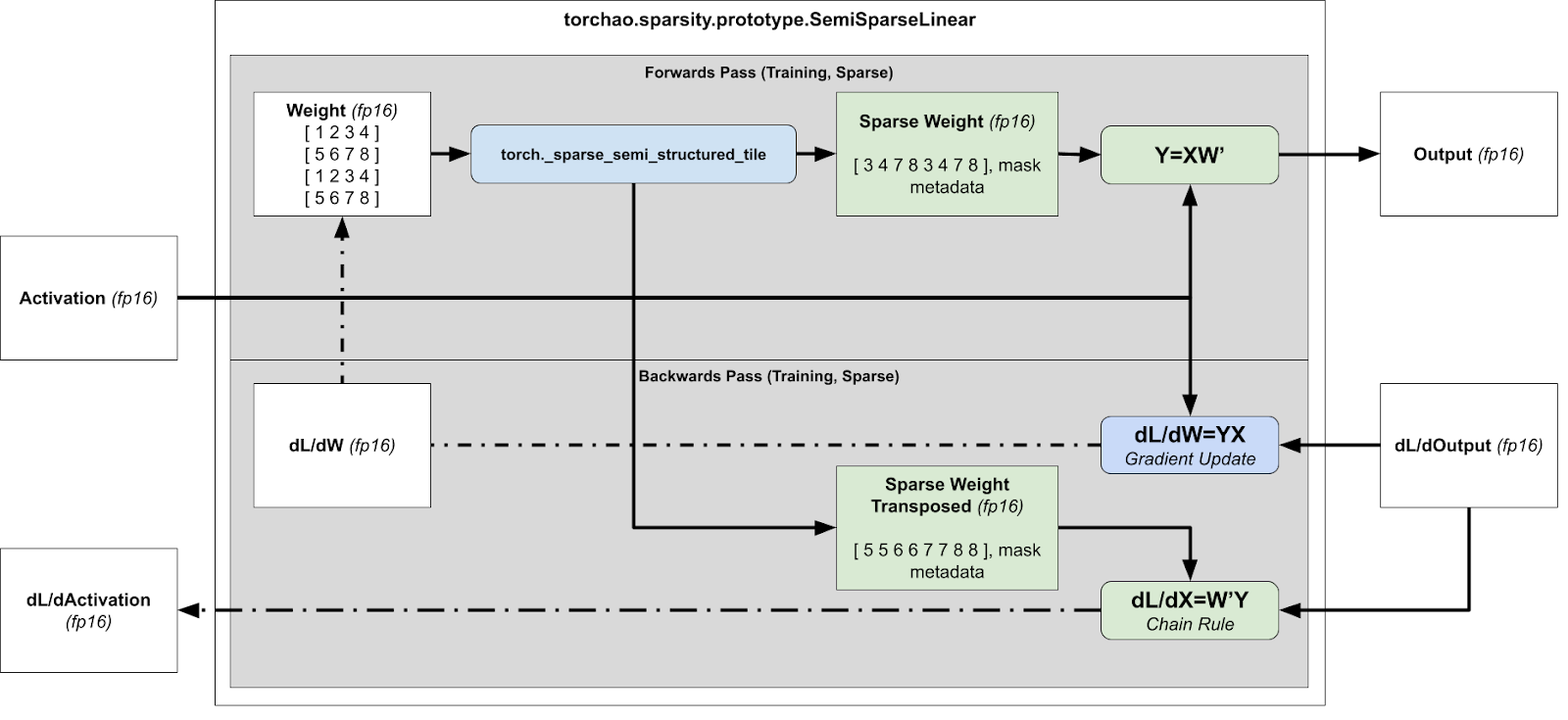
Overview of runtime sparsification for training acceleration (FW + BW pass)

訓練加速執行時稀疏化概述（前向 + 反向傳播）

然而，這有問題，因為壓縮表示無法轉置，因為無法保證張量在兩個方向上都是 2:4 稀疏的。

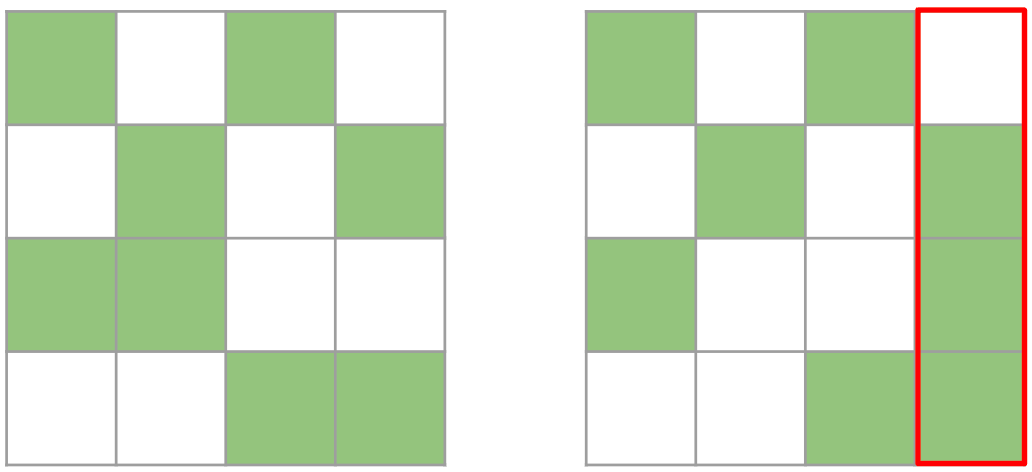
Both matrices are valid 2:4 matrices. However, the right one is no longer a valid 2:4 matrix once transposed because one column contains more than 2 elements

這兩個矩陣都是有效的 2:4 矩陣。然而，右邊的矩陣在轉置後不再是有效的 2:4 矩陣，因為其中一列包含超過 2 個元素。

因此，我們修剪一個 4x4 的塊，而不是一個 1x4 的條帶。我們貪婪地保留最大值，確保每行/每列最多保留 2 個值。雖然這種方法不能保證最優（因為我們有時只保留 7 個值而不是 8 個），但它能有效地計算出一個在行方向和列方向上都是 2:4 稀疏的張量。

然後，我們同時壓縮打包張量和打包轉置張量，並存儲轉置張量用於反向傳播。透過同時計算打包張量和打包轉置張量，我們避免了在反向傳播中的二次核心呼叫。

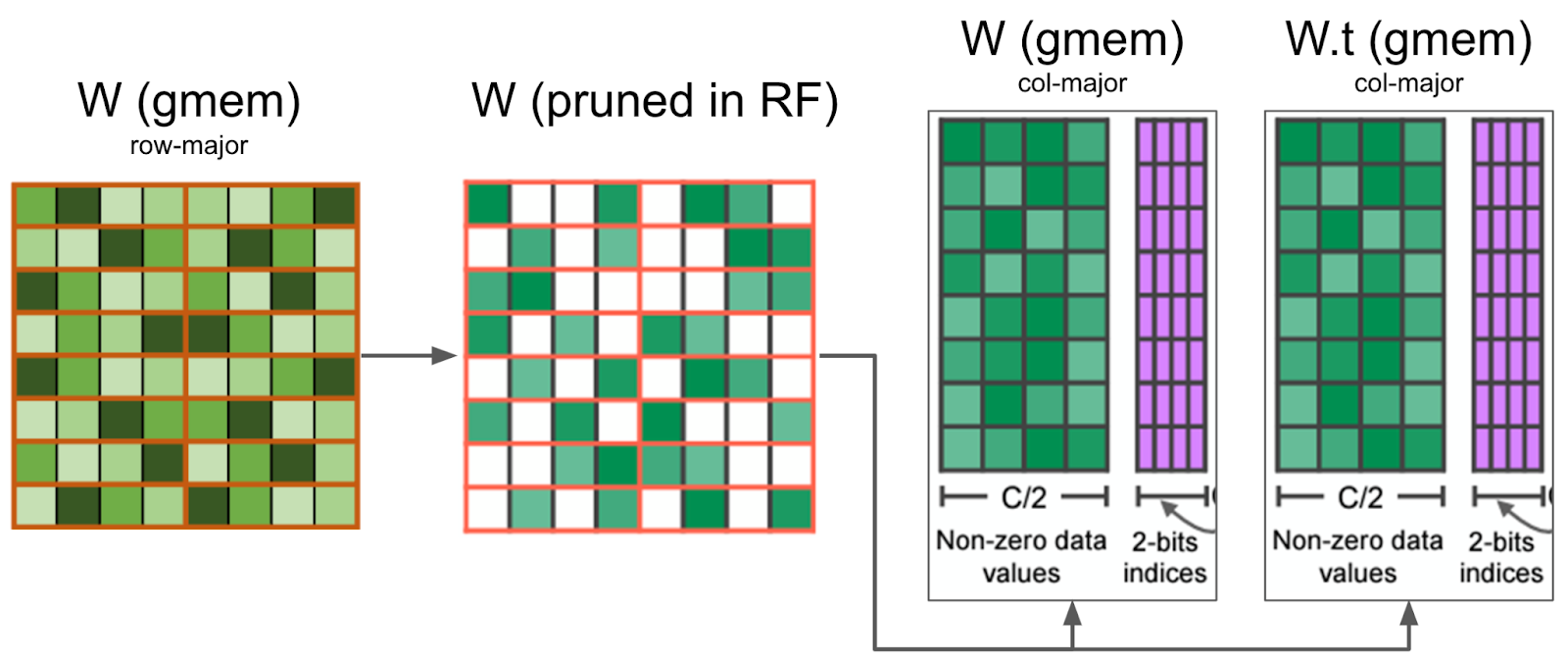
Our kernel prunes the weight matrix in registers

我們的核心在暫存器中修剪權重矩陣，並將壓縮值寫入全域性記憶體。它還同時修剪了反向傳播所需的 W.t，從而最大限度地減少了記憶體 IO。

為了處理反向傳播，還需要一些額外的轉置技巧——底層硬體只支援第一個矩陣是稀疏的操作。對於推理期間的權重稀疏化，當我們計算 xWT 時，我們依賴轉置屬性來交換運算元的順序。

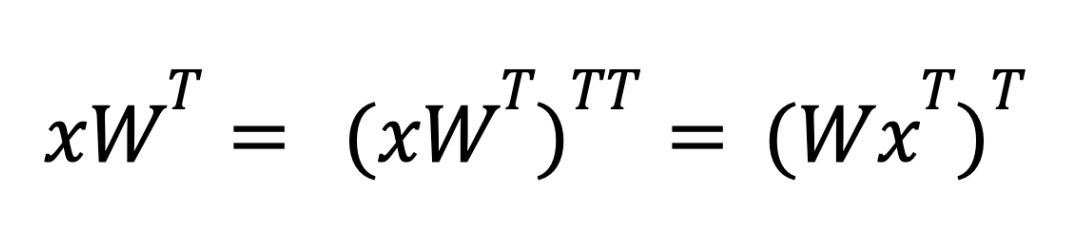
Math formula

在推理過程中，我們使用 `torch.compile` 將外部轉置融合到後續的逐點操作中，以避免效能損失。

然而，在訓練的反向傳播情況下，我們沒有後續的逐點操作可以融合。相反，我們透過利用 cuSPARSELt 指定結果矩陣的行/列布局的能力，將轉置融合到我們的矩陣乘法中。

2) 高效記憶體 IO 的核心分塊

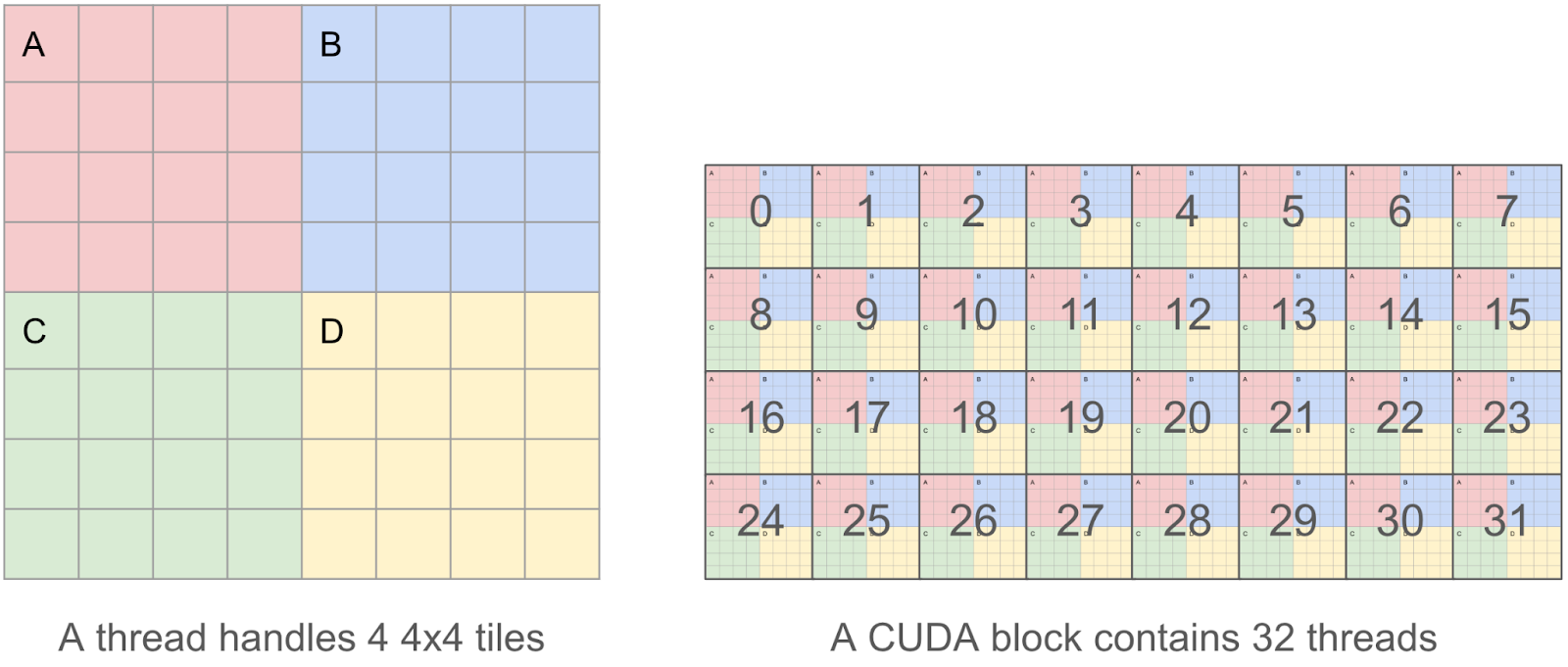
為了使我們的核心儘可能高效，我們希望合併我們的讀/寫操作，因為我們發現記憶體 IO 是主要的瓶頸。這意味著在一個 CUDA 執行緒中，我們希望一次讀/寫 128 位元組的塊，這樣多個並行讀/寫可以被 GPU 記憶體控制器合併為一個請求。

因此，我們決定每個執行緒將處理 4 個 4x4 瓦片（即一個 8x8 瓦片），而不是一個執行緒處理單個 4x4 瓦片（只有 4x4x2 = 32 位元組），這使我們能夠操作 8x8x2 = 128 位元組的塊。

Kernel tiling for efficient memory-IO

3) 在 4x4 瓦片中對元素進行排序而不產生執行緒束分化

對於執行緒中的每個 4x4 瓦片，我們計算一個位掩碼，指定要修剪哪些元素以及要保留哪些元素。為此，我們對所有 16 個元素進行排序並貪婪地保留元素，只要它們不違反我們的 2:4 行/列約束。這隻保留了值最大的權重。

關鍵是，我們觀察到我們只對固定數量的元素進行排序，因此透過使用無分支的 排序網路，我們可以避免執行緒束分化。

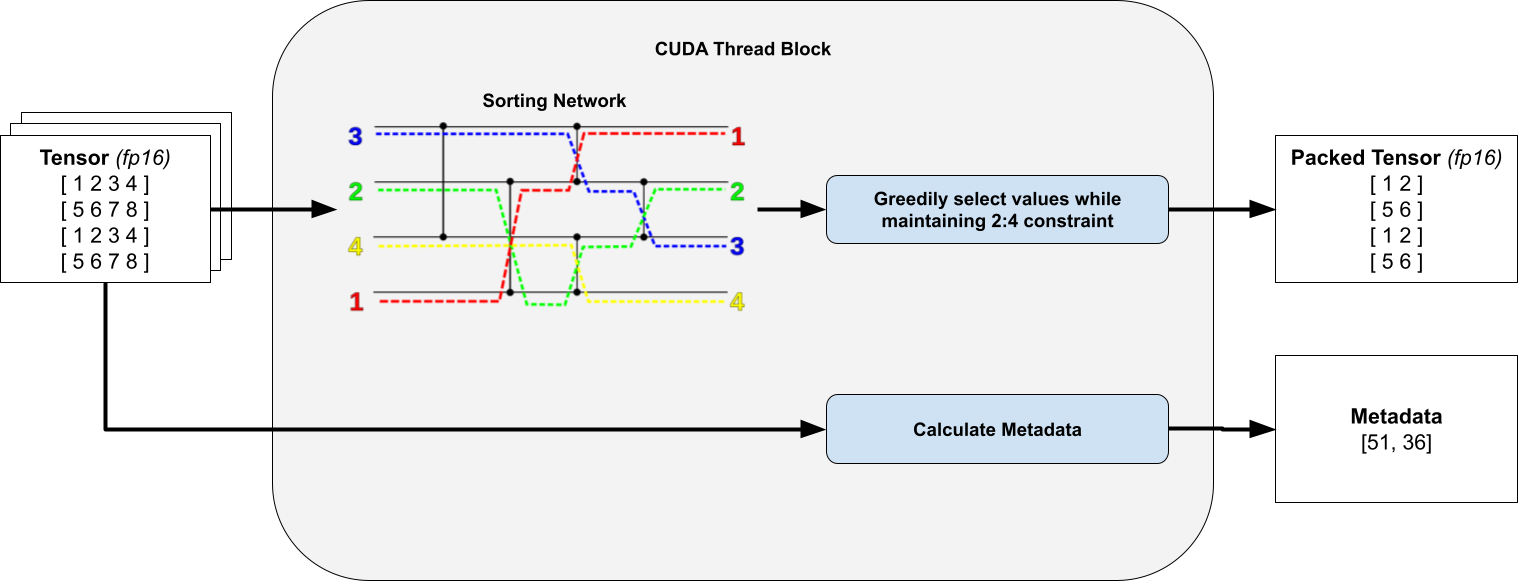
Sorting network diagram

為清晰起見，省略了轉置打包張量和元資料。排序網路圖取自 Wikipedia。

當我們線上程塊中進行條件執行時，會發生執行緒束分化。在 CUDA 中，同一工作組（執行緒塊）中的工作項在硬體級別以批次（執行緒束）分派。如果存在條件執行，使得同一批次中的某些工作項執行不同的指令，那麼當執行緒束被分派時，它們會被遮蔽，或者按順序分派。

例如，如果我們的程式碼是 `if (condition) do(A) else do(B)`，其中所有奇數工作項都滿足 condition，那麼此條件語句的總執行時間是 `do(A) + do(B)`，因為我們會為所有奇數工作項分派 `do(A)`，遮蔽偶數工作項，併為所有偶數工作項分派 `do(B)`，遮蔽奇數工作項。此 答案 提供了有關執行緒束分化的更多資訊。

4) 寫入壓縮矩陣和元資料

一旦位掩碼計算完畢，權重資料必須以壓縮格式寫回全域性記憶體。這並非易事，因為資料需要保留在暫存器中，並且無法索引暫存器（例如 `C[i++] = a` 會阻止我們將 `C` 儲存在暫存器中）。此外，我們發現 `nvcc` 使用的暫存器比我們預期的要多得多，這導致暫存器溢位並影響了整體效能。我們將此壓縮矩陣以列主序格式寫入全域性記憶體，以提高寫入效率。

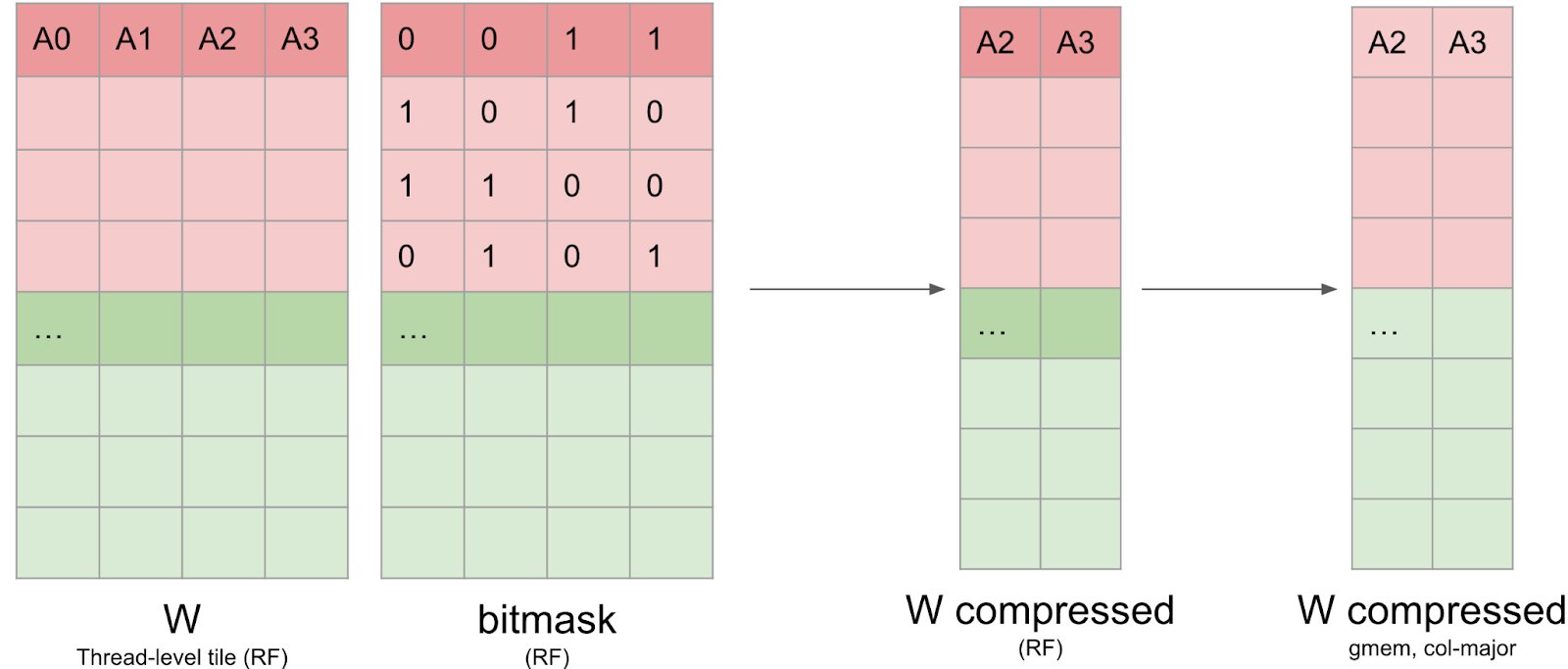
compressed matrix to global memory in Column-Major format

我們還需要寫入 cuSPARSELt 元資料。此元資料佈局與開源 CUTLASS 庫的佈局非常相似，並且經過最佳化，可以透過 PTX `ldmatrix` 指令在 GEMM 核心中高效載入共享記憶體。

然而，此佈局並未最佳化以高效寫入：元資料張量的前 128 位包含有關第 0、8、16 和 24 行的前 32 列的元資料。回想一下，每個執行緒處理一個 8x8 瓦片，這意味著此資訊分散在 16 個執行緒中。

我們依賴一系列執行緒束混洗操作，分別用於原始表示和轉置表示以寫入元資料。幸運的是，此資料僅佔總 IO 的不到 10%，因此我們可以承受不完全合併寫入的代價。

DINOv2 稀疏訓練：實驗設定與結果

在我們的實驗中，ViT-L 模型使用 DINOv2 方法在 ImageNet 上訓練了 125k 步。我們所有的實驗都在 4 個 AMD EPYC 7742 64 核 CPU 和 4 個 NVIDIA A100-80GB GPU 上執行。在稀疏訓練期間，模型在前一部分訓練中啟用了 2:4 稀疏性，其中只有一半的權重被啟用。權重的稀疏掩碼在訓練過程的每一步都會動態重新計算，因為權重在最佳化過程中會不斷更新。在剩餘的步驟中，模型進行密集訓練，生成一個最終沒有 2:4 稀疏性的模型（除了 100% 稀疏訓練設定），然後進行評估。

訓練設定ImageNet 1k 對數迴歸
0% 稀疏（125k 密集步，基線）82.8
40% 稀疏（50k 稀疏 -> 75k 密集步）82.9
60% 稀疏（75k 稀疏 -> 50k 密集步）82.8
70% 稀疏（87.5k 稀疏 -> 37.5k 密集步）82.7
80% 稀疏（100k 稀疏 -> 25k 密集步）82.7
90% 稀疏（112.5k 稀疏 -> 12.5k 密集步）82.0
100% 稀疏（125k 稀疏步）82.3（2:4 稀疏模型）
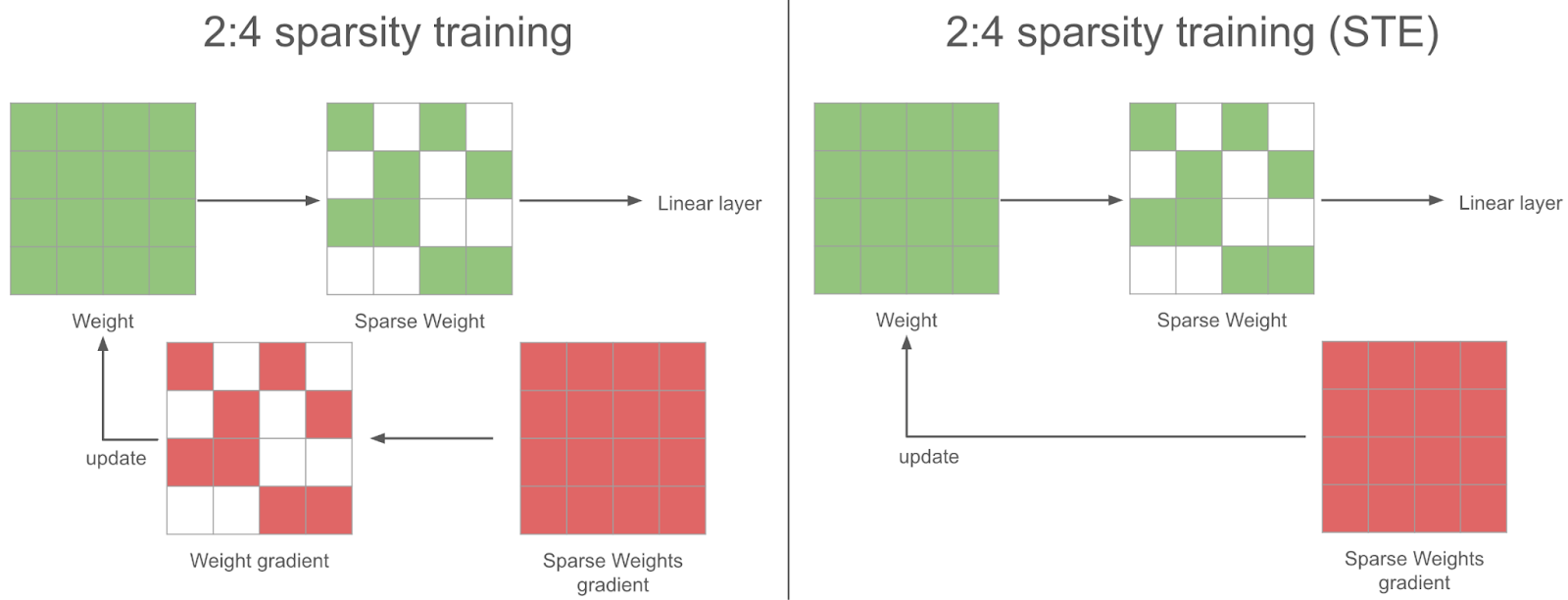
sparsity training diagrams

在稀疏訓練步驟中，在反向傳播過程中，我們獲得了稀疏權重的密集梯度。為了使梯度下降合理，我們也應該在將其用於最佳化器更新權重之前稀疏化此梯度。相反，我們使用完整的密集梯度來更新權重——我們發現這在實踐中效果更好：這就是 STE（Straight Through Estimator）策略。換句話說，我們每一步都會更新所有引數，即使是我們不使用的引數。

結論與未來工作

在這篇部落格文章中，我們展示瞭如何利用半結構化稀疏性加速神經網路訓練，並解釋了我們面臨的一些挑戰。我們成功地在 DINOv2 訓練中實現了 6% 的端到端加速，且準確率僅下降了 0.1 個百分點。

這項工作有幾個擴充套件領域：

  • **擴充套件到新的稀疏模式：** 研究人員已經建立了新的稀疏模式，如 V:N:M 稀疏性，它們使用底層半結構化稀疏核心來實現更大的靈活性。這對於將稀疏性應用於大型語言模型（LLM）尤其有趣，因為 2:4 稀疏性會導致準確性下降過多，但我們已經看到了更一般的 N:M 模式的積極 結果。
  • **稀疏微調的效能最佳化：** 這篇文章涵蓋了從頭開始的稀疏訓練，但通常我們希望微調一個基礎模型。在這種情況下，靜態掩碼可能足以保持準確性，這將使我們能夠進行額外的效能最佳化。
  • **更多關於剪枝策略的實驗：** 我們在網路的每一步計算掩碼，但每 n 步計算一次掩碼可能會產生更好的訓練準確性。總的來說，找出在訓練過程中使用半結構化稀疏性的最佳策略是一個開放的研究領域。
  • **與 fp8 的相容性：** 硬體也支援 fp8 半結構化稀疏性，原則上這種方法應該與 fp8 類似地工作。實際上，我們需要編寫類似的稀疏化核心，並可能將其與張量縮放融合。
  • **啟用稀疏性：** 高效的稀疏化核心還可以在訓練期間稀疏化啟用。由於稀疏化開銷隨稀疏矩陣大小線性增長，因此與權重張量相比，具有大啟用張量的設定可以從啟用稀疏性中獲得比權重稀疏性更多的益處。此外，由於使用了 ReLU 或 GELU 啟用函式，啟用天然是稀疏的，從而減少了準確性下降。

如果您對這些問題感興趣，請隨時在 torchao 中提出問題/PR，這是一個我們正在為量化和稀疏性等架構最佳化技術構建的社群。此外，如果您對稀疏性普遍感興趣，請在 CUDA-MODE (#sparsity) 中聯絡我們。