在這篇部落格文章中,我們探討了論文 “快速而簡潔:Triton 中的 2-單純注意力” [1] 中提出的核心設計細節。我們首先用硬體對齊的設計對 2-單純注意力演算法進行建模,然後使用現代 GPU 核心技術,在 TLX (Triton Low-Level Extensions) [2] 中完全重寫了整個核心。利用 TLX,我們成功地在 NVIDIA H100 GPU 上實現了 2-單純注意力前向傳播中高達 588 Tensor Core BF16 TFLOPs,大約 60% 的 Tensor Core 利用率,這比原始 Triton 核心的 337 峰值 TFLOPs 提升了約 1.74 倍的速度。
程式碼庫:https://github.com/pytorch/FBGEMM/tree/main/fbgemm_gpu/experimental/simplicial_attention
† 在 Meta 工作期間完成
2-單純注意力回顧
隨著大型語言模型的不斷擴充套件,獲取足夠高質量的訓練詞元變得越來越具有挑戰性。提高注意力機制的詞元效率對於解決這個問題至關重要。一個很有前途的進展是 2-單純注意力(演算法 1),它使用三線性函式來建模查詢與兩組鍵(K1、K2)和兩組值(V1、V2)之間的互動,以建模詞元三元組之間複雜的互動,而不是像標準點積注意力那樣只建模詞元對。正如論文《邏輯與 2-單純 Transformer》[3] 中首次提出的那樣,2-單純注意力在基本保持原始模型大小的同時增加了注意力的 TFLOPs。根據縮放律實驗,2-單純注意力在詞元效率方面顯示出顯著改進,特別是在數學和邏輯問題解決等推理任務中。

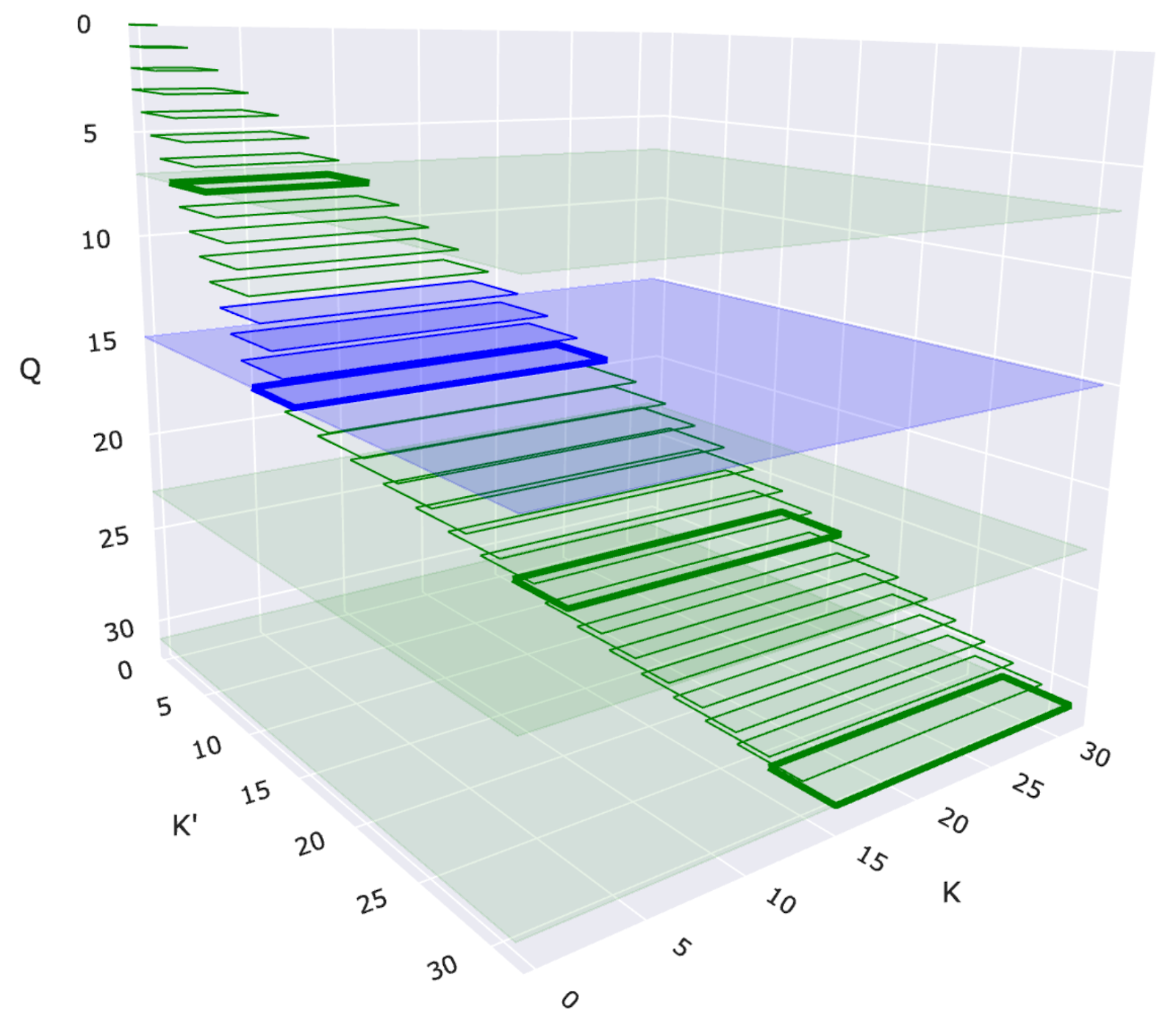
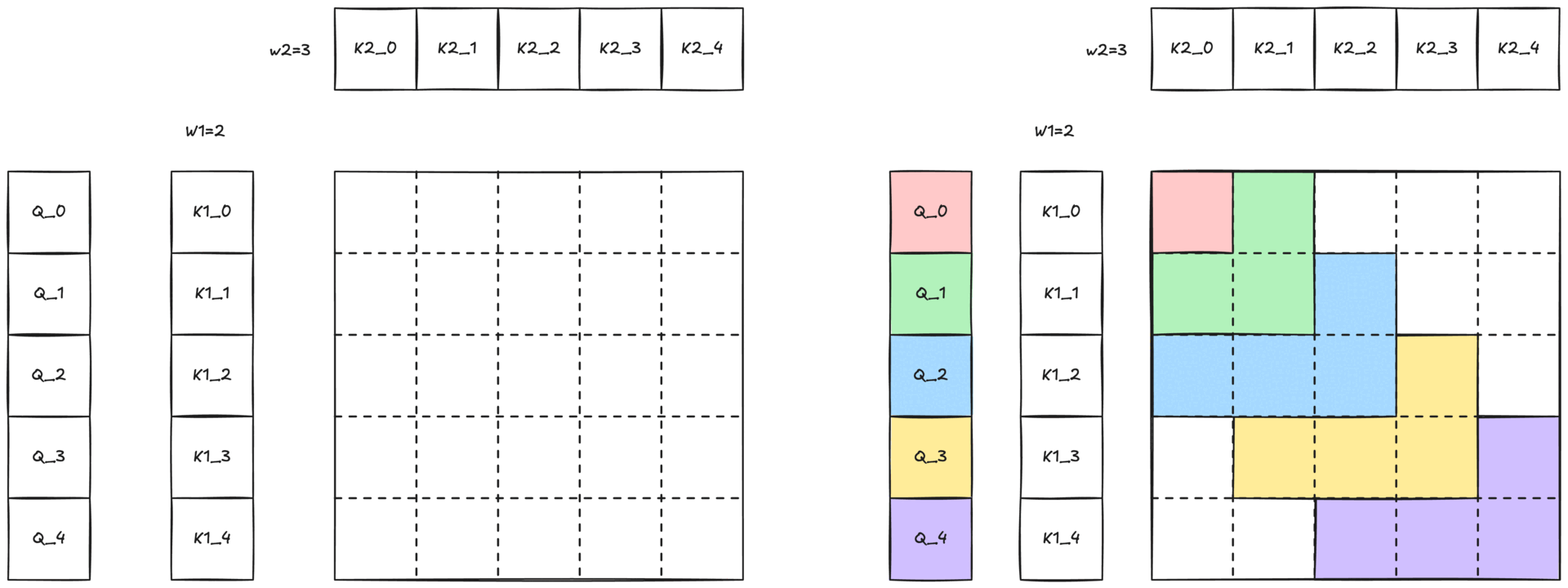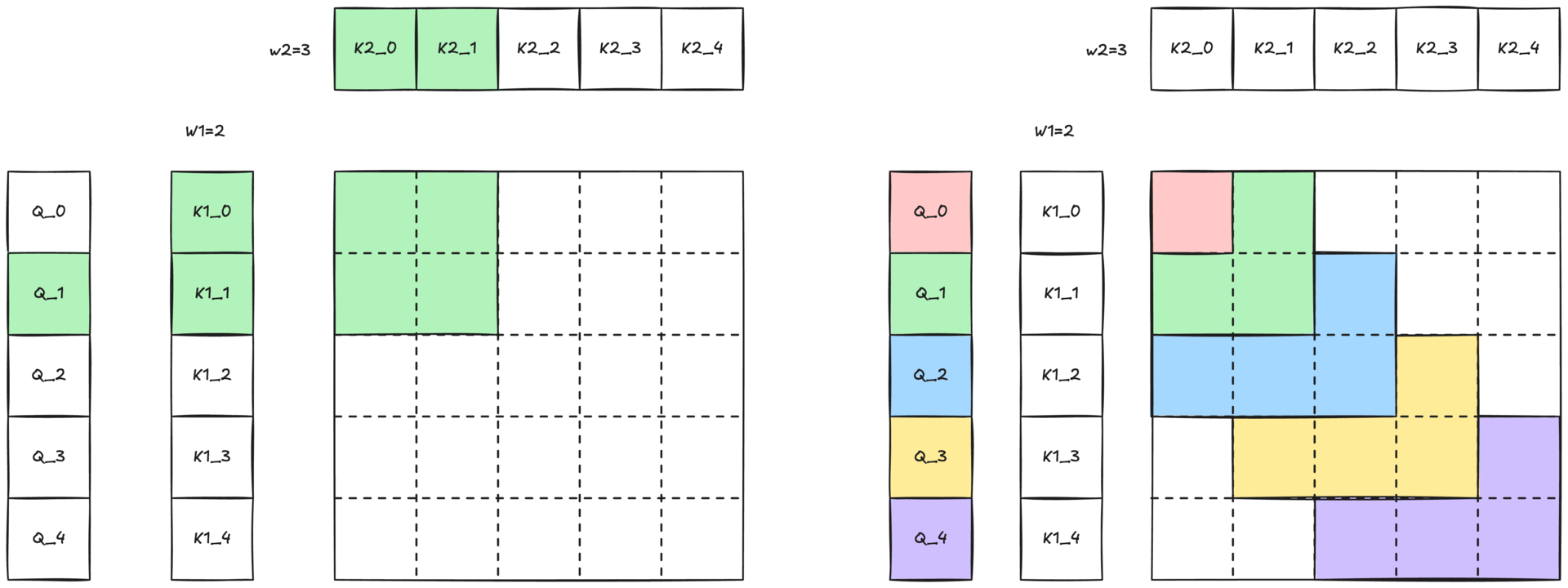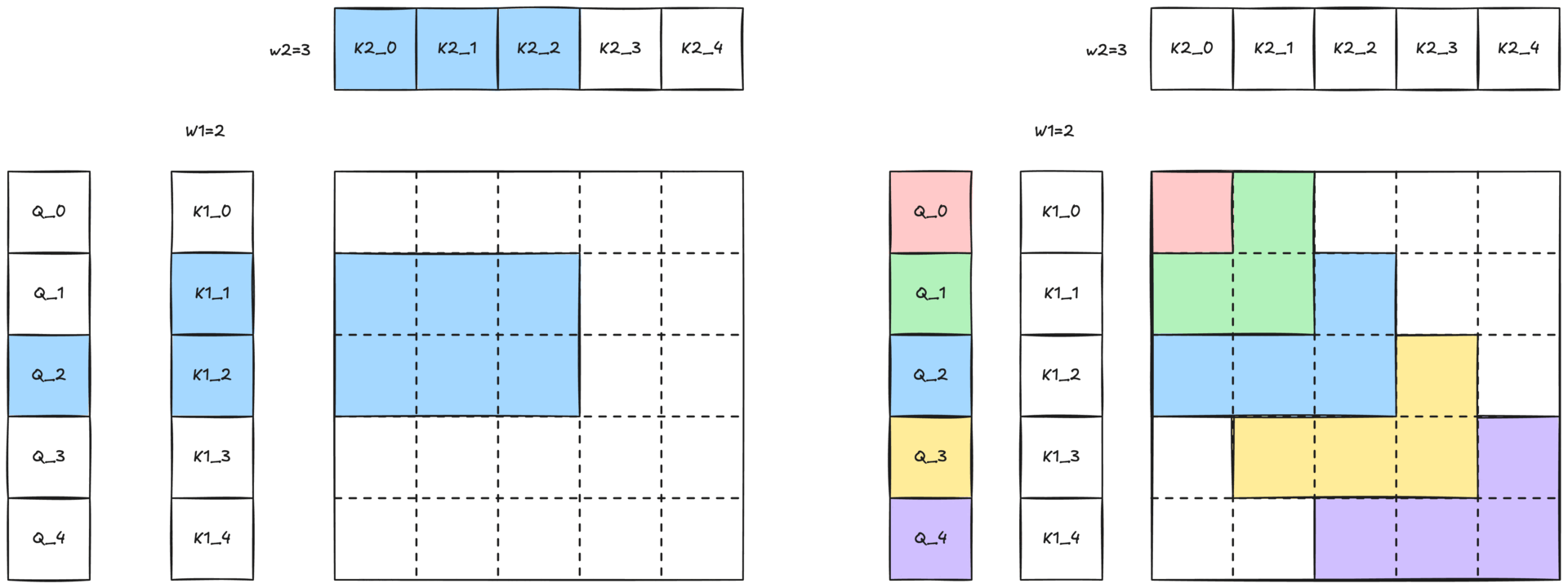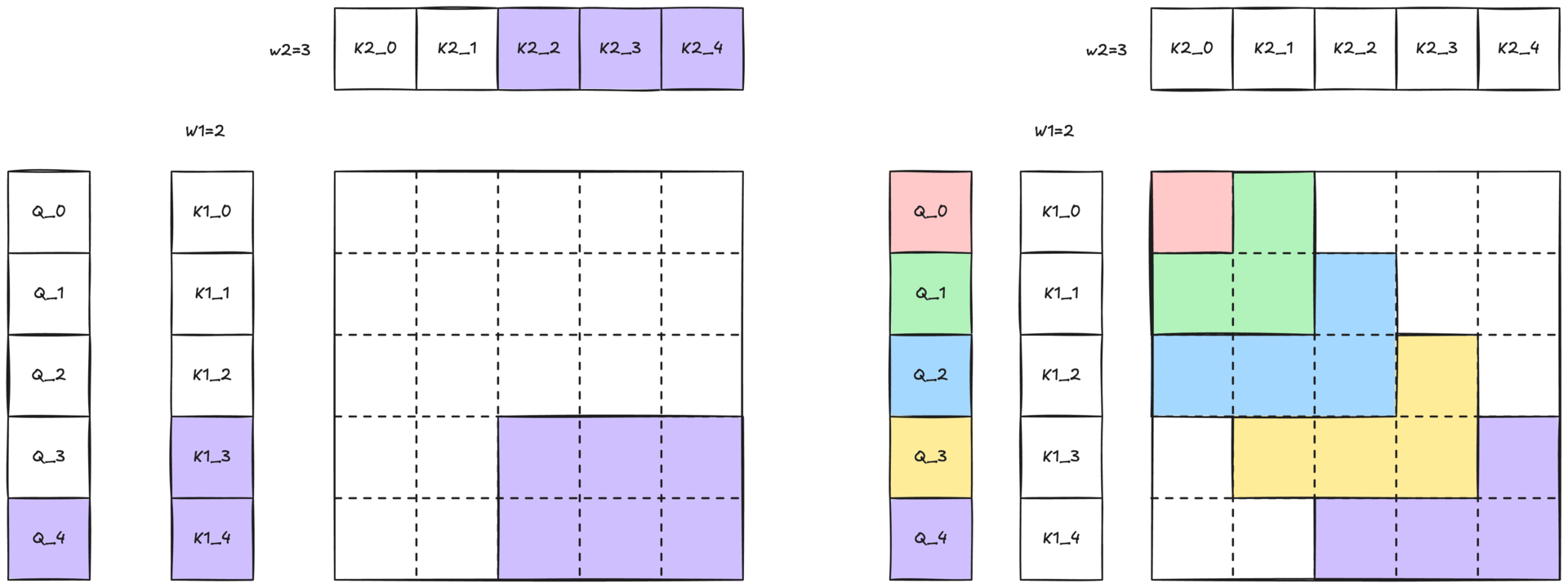
圖 1:帶有二維滑動視窗的 2-單純注意力視覺化。每個矩形表示一個查詢 (Q) 和一對鍵 (K' 和 K) 之間的互動。藍色矩形突出顯示滑動視窗結構中特定的查詢-鍵對互動。
二維滑動視窗注意力
圖 2:滑動視窗注意力與 2-單純滑動視窗注意力的比較
由於完整的 2-單純注意力會隨著序列長度呈三次增長 O(N³),因此處理整個序列是不切實際的。我們透過一個由兩個視窗大小 W1 和 W2 定義的二維滑動視窗(如圖 2-b 所示,並在圖 1 中展示)來減輕這種成本。每個查詢詞元 Q[i] 只關注
- 沿第一維最近的 W1 個 K1[i] / V1[i] 對
- 沿第二維最近的 W2 個 K2[k] / V2[k] 對
這種區域性性約束保持了 2-單純注意力的表達能力,同時使計算變得可行。
圖 3:帶有二維滑動視窗的 2-單純注意力示意圖。與 Q 詞元顏色相同的彩色區域表示查詢可以關注鍵和值的二維鄰域 (W1 × W2)。
TLX – Triton 低階擴充套件介紹
TLX (Triton Low-Level Extensions) 是 Triton DSL 的語言擴充套件,它結合了高效能和開發者生產力。它與 Triton 的高階 Python API 無縫整合,同時透過一組豐富的內部函式,為 GPU 核心執行添加了面向 warp 的、接近硬體的控制。TLX 原生支援 NVIDIA Hopper 和 Blackwell 架構,並具有可擴充套件的設計以支援未來的架構,包括潛在的 AMD GPU,它支援共享記憶體平鋪、暫存器支援的累加器、warp 專用化、流水線執行和細粒度 warp 級同步。
快速 2-單純注意力 – 硬體對齊設計
為了使核心真正高效並實現 SOTA 效能,我們在模型和核心之間進行了大量硬體對齊的協同設計。所提出的核心設計採用以下關鍵特性。
Tensor Core 友好
由於點積本質上是兩個張量之間的二元運算 (dot_product),2-單純注意力(詳見附錄 [3])中存在三個張量 (trilinear_product) 提出了一個根本性挑戰:計算 無法 直接利用 Tensor Core。
為了解決這個限制,我們透過戰略性預計算開發了一種 Tensor Core 相容的方法。我們的解決方案將 三元 運算分解為 二元 元件:
- 首先,我們預計算 Q[i] 和 K1[s] 的元素乘積(公式 (c) 第 10 行),從而實現後續與 K2[t] 的乘法(公式 (c) 第 11 行)的 Tensor Core 計算。
- 類似地,我們預計算 V1[s] 和 V2[t] 的元素乘積(公式 (c) 第 13 行),允許高效地使用組合的 V12[s][t] 進行 P 的 Tensor Core 計算(公式 (c) 第 14 行)。
這種重新表述(如 公式 (c) 所示)將 2-單純滑動視窗注意力轉換為 Tensor Core 友好 的設計,並保持了數學等價性。

注意: ⊙ 表示元素級乘法
我們考慮了兩種方法來實現 Tensor Core 友好的 GPU 核心公式
- 單獨的核心:在一個核心中實現預計算,將結果 (Precomputed-QK1 和 Precomputed-V1V2) 寫入全域性記憶體 (GMEM),並使用自定義的點積注意力核心。
- 融合核心:將整個公式 (c) 整合到一個注意力核心中。
第一種方法存在一個顯著的缺點:峰值記憶體使用量大幅增加。具體來說,Precomputed-QK1 需要比 Q 多 W1 倍的記憶體,而 Precomputed-V1V2 需要比 V 多 (W1 + W2) 倍的記憶體。對於典型值,例如 W1 = 32,W2 = 512,並且 N 隨著模型的上下文視窗縮放,記憶體開銷對於包含 2-單純注意力的模型訓練來說變得 prohibitive。因此,我們採用了第二種方法,實現了一個用於 2-單純滑動視窗注意力的端到端融合核心。
非對稱滑動視窗
非對稱滑動視窗 (W1 ≠ W2) 與 對稱滑動視窗 (W1 = W2):實驗結果 [1] 表明,當 W1 x W2 保持不變(保持相同的 Tensor Core TFLOPs)時,非對稱配置通常會產生更好的模型質量。為了硬體對齊,我們採用較小的 W1 和較大的 W2 值(在我們的實現中 W1 = 32,W2 = 512),原因如下:
- Tensor Core 友好:較大的 W2 值增加了 Tensor Core 與 CUDA Core 的比率,提高了 Tensor Core 計算效率。
- 在共享記憶體 (SMEM) 中保留所有 K1 和 V1 瓦片:根據演算法 2,每個 K1/V1 瓦片形狀為 [1, D],需要 W1 次載入。對於較小的 W1,我們可以在迴圈外將所有 W1 個 K1/V1 瓦片以 [W1, D] 的形狀載入到 SMEM 中,然後在 W1 迴圈期間將單個 [1, D] 瓦片從 SMEM 重新載入到暫存器中。對於 W1 = 32,D = 128,以及 BFloat16 精度,K1 和 V1 瓦片的總大小為 16KB,約佔 H100 SMEM 容量的 7%。
頭部組平鋪 – Pack GQA
在滑動視窗注意力中,每個查詢 Q 詞元選擇不同的 K 詞元集。當沿著序列維度進行平鋪時,我們必須遮蔽掉某些 QK 對,導致計算浪費。這種低效率在 2D 滑動視窗注意力中被放大。例如,在 BLOCK_M = 64,BLOCK_KV = 128,N = 8192,W1 = 32 和 W2 = 512 的情況下,根據附錄 [1] 中的計算。大約 73.2% 的計算被浪費。
受 Native Sparse Attention [5] 核心設計的啟發,我們將同一 GQA KV 頭組的所有查詢頭打包到一個瓦片中,而不是沿著序列維度進行平鋪。這種方法消除了大部分二維滑動視窗掩碼計算。在我們最終的實現中,滑動視窗掩碼僅在最初幾個 CTA 的最後一個 W2 迴圈迭代中需要,將浪費率從 73.2% 降低到 1.35%(詳細計算見附錄 [1])。
權衡考慮:頭部維度平鋪的缺點是查詢頭數量配置的靈活性降低。WGMMA [6] 指令要求最小 M = 64。低於 64 的配置也會浪費計算。為了平衡掩碼效率和模型靈活性,我們可以將連續的 Q 詞元與 Q 頭打包到一個瓦片中,以滿足 64 大小要求(類似於 FA3 解碼核心中的 PACK_GQA)。雖然原始論文使用 GQA 比率 64,但我們的實現使用 128,以在不同的 Q 瓦片上實現兩個消費者 warp-group 分割槽,用於峰值 TFLOPs 的基準測試。
V1 瓦片最佳化
考慮操作 C = A @ B。WGMMA 指令允許矩陣 A 儲存在暫存器記憶體 (RMEM) 或 SMEM 中,而矩陣 B 必須駐留在 SMEM 中。輸出瓦片 C 儲存在 RMEM 中。對於注意力中的 PV12 GEMM,P(QK12 GEMM 的輸出)駐留在 RMEM 中,V2(透過 TMA 載入)駐留在 SMEM 中。然而,V1 和 V2 公式 (c) 的廣播乘法操作要求兩個運算元都在 RMEM 中。這需要將 V2 從 SMEM 載入到 RMEM,執行元素級計算生成 V12,然後將 V12 儲存回 SMEM。這是一個低效的過程。
我們觀察到 PV GEMM 的輸出駐留在 RMEM 中,並且由於 V1 沿著 PV12 的點積維度廣播,因此在與 P 進行點積之前或之後應用 V1 到 V2 在數學上是等價的。
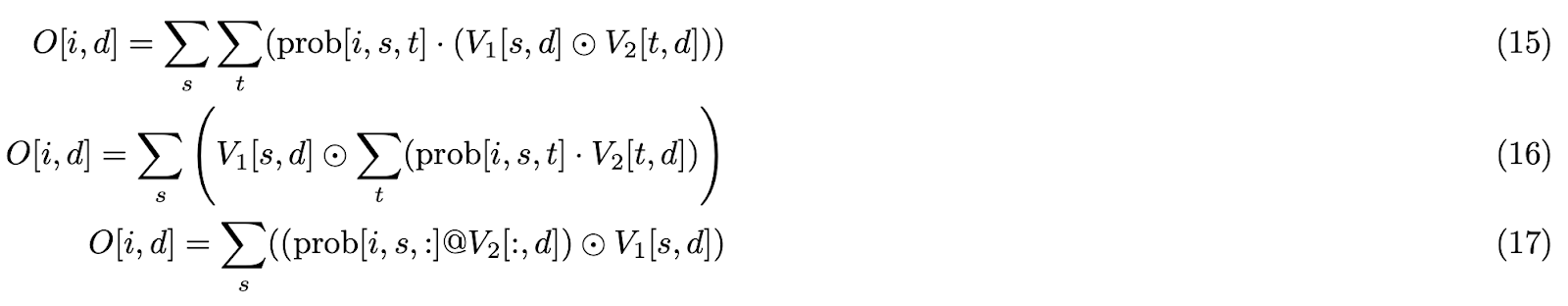
因此,我們優化了演算法,將 V1 瓦片直接應用於 PV GEMM 輸出,消除了冗餘的 SMEM ↔ RMEM 載入/儲存操作。
注意: 為什麼計算 Q⊙K1 而不是 K1⊙K2?因為
- K1⊙K2 無法在 w1 迴圈中預計算。預計算所有組合需要將大小為 w1 × w2 × D 的資料儲存在 SMEM 中,這太大了,無法容納。
- K1⊙K2 的結果駐留在 RMEM 中,造成了與 V1⊙V2 相同的低效率。
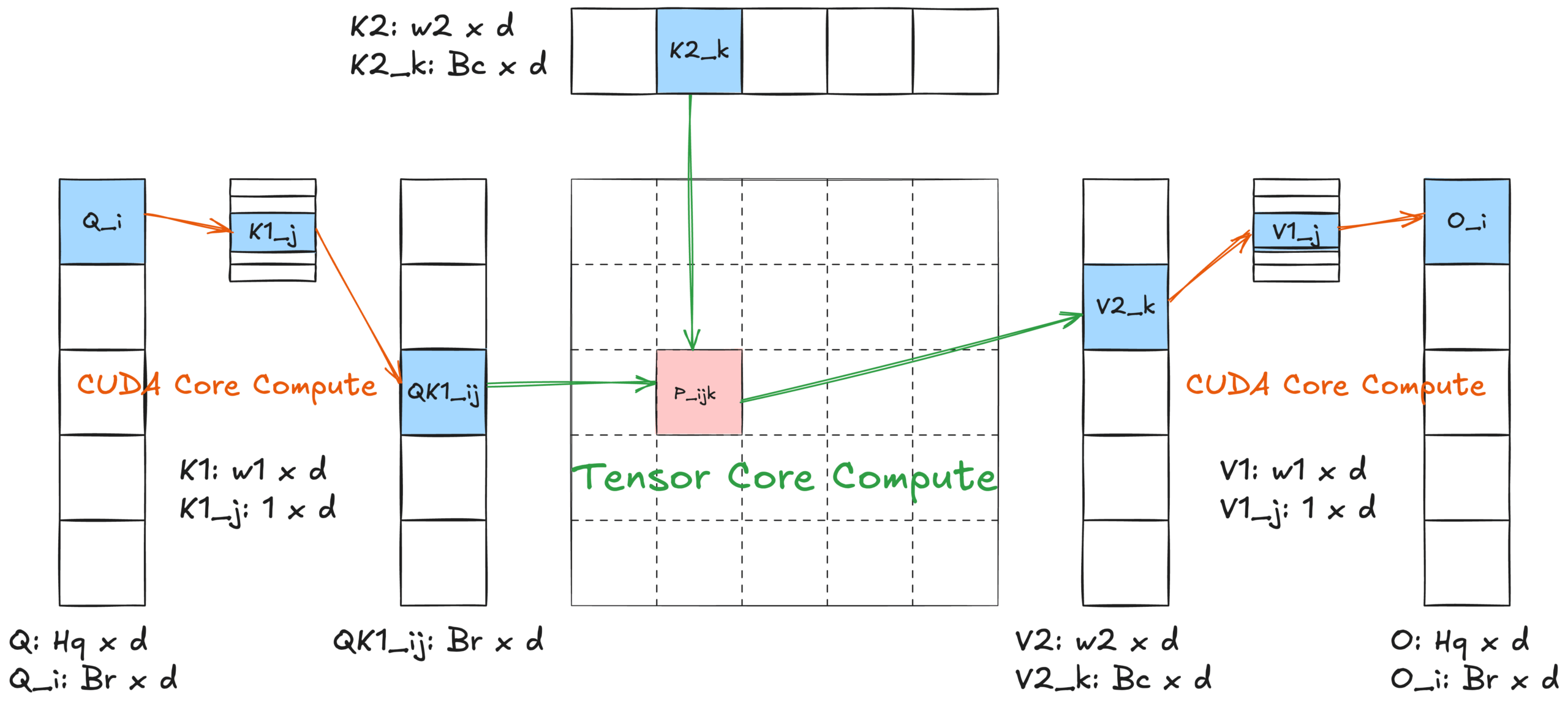
圖 4:演算法 2 核心設計示意圖
基於所有這些特性和 FlashAttention2 [3] 演算法,我們實施了融合的 2-單純注意力核心演算法——演算法 2。與點積注意力相比,它引入了兩個巢狀的 w1 和 w2 內迴圈,其中最內層迴圈與 FlashAttention2 的內迴圈非常相似。

演算法 2 進行了更多的 CUDA Core 計算,引發了 CUDA Core 是否會成為 2-單純注意力核心效能瓶頸的問題。我們的分析表明 CUDA Core 不是限制因素;詳細論證在附錄 [5] 中提供。
採用 TLX 的現代 GPU 技術
儘管實施了上述所有最佳化,我們的 Triton 核心實現仍遠低於最先進的效能。我們最佳的前向注意力核心只能實現 34% 的 Tensor Core 利用率,而 FlashAttention3 [4] 擁有令人印象深刻的 75% 利用率。
對生成的 PTX 程式碼的分析顯示,軟體流水線和自動 warp 專用化未能與核心協同工作。軟體流水線編譯器後端無法執行必要的模式匹配並跳過了最佳化,而 warp 專用化則觸發了 2-單純注意力實現特有的編譯錯誤。
為了在 Hopper 架構上快速整合 FlashAttention3 [4] 等現代注意力最佳化技術,包括 warp 專用化、跨 warpgroup 重疊(乒乓排程)和 warpgroup 內重疊(計算流水線),我們使用 TLX 重寫了核心。我們開發了三個不同的版本:
- 核心 1:前向 + Warp 專用化(附錄 [4] 演算法 3 中描述)
- 核心 2:前向 + Warp 專用化 + 計算流水線
- 核心 3:前向 + Warp 專用化 + 乒乓排程
注意: 如果您想了解更多關於 Hopper 上的 Warp 專用化、計算流水線和乒乓排程,請參閱論文 FlashAttention3 [4] 和 Colfax 部落格。
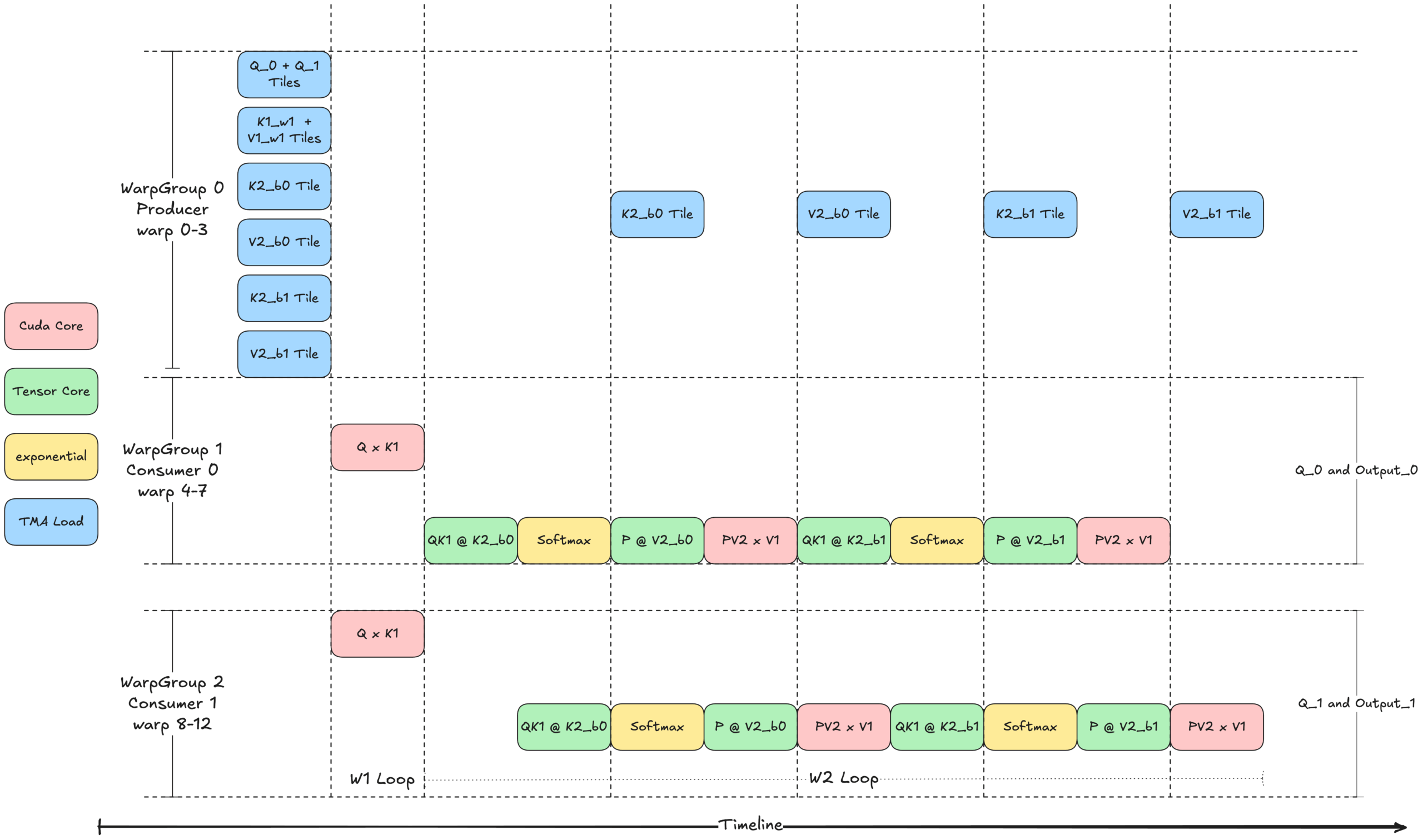
圖 5 展示了核心 3 的思想:帶有乒乓排程的 Warp 專用化,使用共享記憶體 (SMEM) 中的兩個緩衝區和兩個消費者組。生產者 (WarpGroup 0) 首先發出 TMA 載入指令,用於兩個 Q 瓦片、一個 K1 瓦片、一個 V1 瓦片以及兩個 K2 和 V2 瓦片。消費者 warp 組等待相應的瓦片到達後執行計算。生產者和消費者之間的同步透過屏障進行管理。
每個消費者組在不同的 Q 瓦片上操作,但共享相同的 K1、V1、K2 和 V2 瓦片,同時為不同的輸出瓦片生成結果。為了最大限度地提高效率,乒乓排程確保在任何時候只有一個 warp 組執行 Tensor Core (WGMMA) 操作。
圖 6 是核心 1 WS(頂部)和帶有乒乓排程的核心 3 WS(底部)的執行軌跡比較圖,使用 Proton [8] 捕獲。這些軌跡突出顯示了乒乓排程如何減少內部 w2 迴圈中的 Tensor Core 氣泡,從而提高 Tensor Core 資源的利用率。
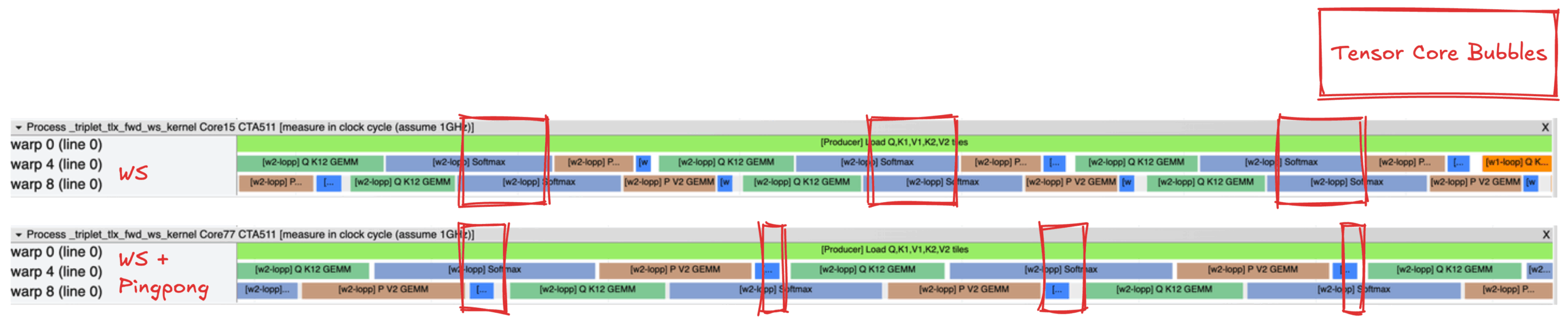
圖 6:核心 1 WS(頂部)和核心 3 WS + 乒乓(底部)的 Tensor Core 氣泡示意圖
基準測試結果顯示,從核心 1 到核心 3,效能提升約為中性到 1%。微小的增益可能反映了核心 1 已經實現了 GEMM 和 Softmax 操作之間的部分重疊。目前,核心 1 實現了 60% 的 Tensor Core 利用率,這比之前純 Triton 實現的 34% Tensor Core 利用率有了顯著提升。核心 2 由於暫存器溢位問題導致效能下降。理論上,Warp 專用化、計算流水線和乒乓排程的結合應該會產生最佳效能。
基準測試
根據附錄 [5] 中的分析,Tensor Core TFLOPs 顯著超過 CUDA Core TFLOPs。因此,為簡化起見,我們僅將 Tensor Core TFLOPs 作為核心效能的主要指標。
請注意 2D 滑動視窗注意力的以下行為,這裡我們假設 W1 ≤ W2:
- 當總序列長度 N < W1 時:該機制在 W1 和 W2 上均作為 2D 因果注意力執行。
- 當 W1 ≤ N < W2 時:該機制在 W1 上作為 1D 滑動視窗執行,在 W2 上作為 1D 因果注意力執行。
- 當 N ≥ W2 時:該機制作為完整的 2D 滑動視窗執行。
有關 Tensor Core TFLOPs 計算的詳細資訊,請參閱附錄 [2]。
基準測試設定詳見 [9]。我們在圖 5 中展示了峰值 588 TFLOPs 的結果。
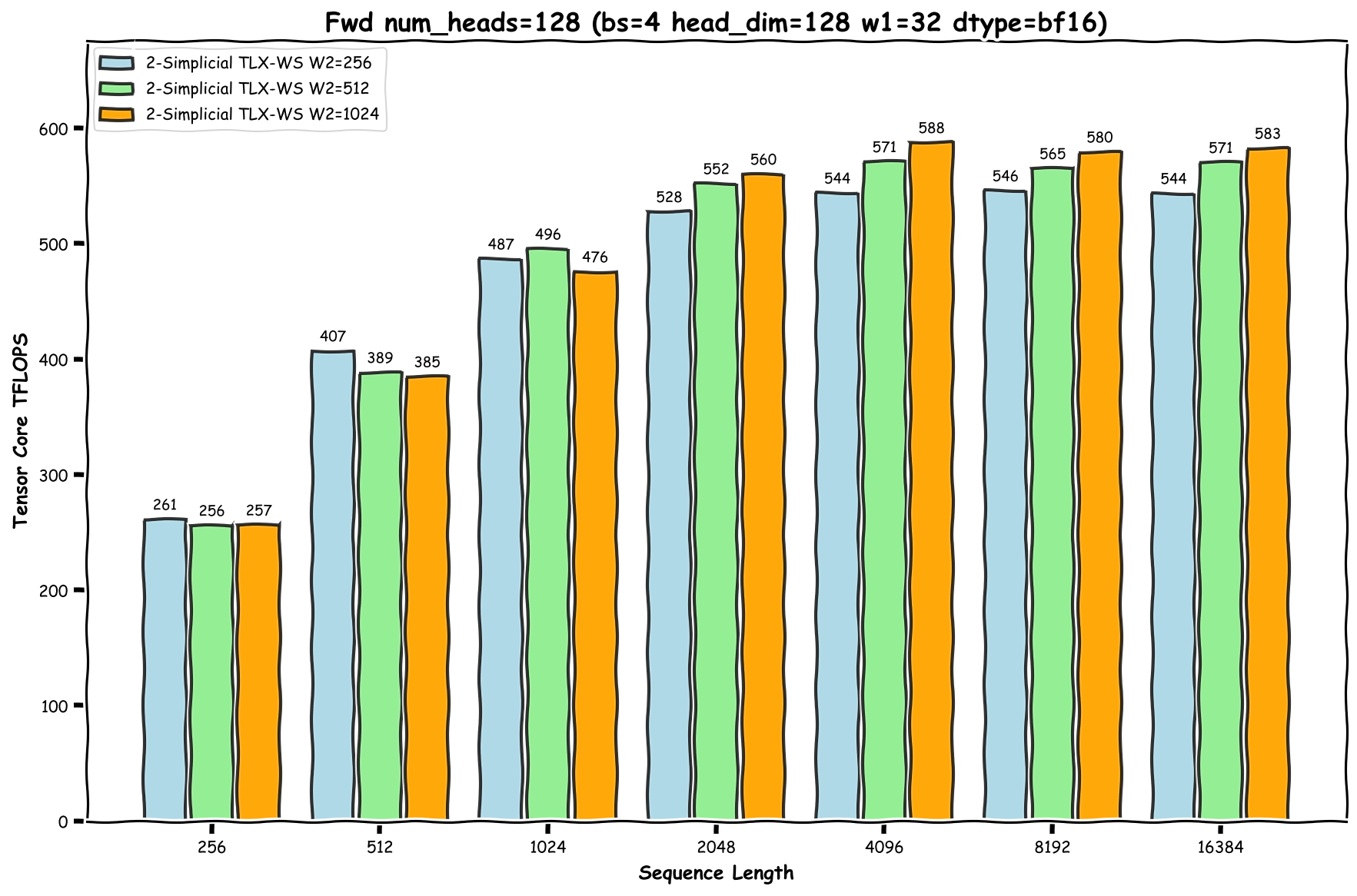
圖 7:快速 2-單純注意力核心 - 前向傳播的基準測試結果
注意:短序列長度會導致效能不佳,因為存在掩碼瓦片。具體來說,對於 i < W2 的詞元,必須對最終瓦片應用因果掩碼以確保 j ≤ i。這會降低這些詞元最終瓦片的計算密度,並增加掩碼計算帶來的 cuda core 開銷。相反,對於 i ≥ W2 且 W2 % BLOCK_KV = 0 的詞元,我們可以從 i-W2+1 迴圈到 i,而無需掩碼,因為所有瓦片都是完整的。由於短序列長度中 i < W2 的詞元比例更高,因此整體效能會受到影響。
我們使用 FlashAttention3 (FA3) 作為點積注意力的參考實現。為了確保每個查詢詞元具有相同的計算工作負載,具體來說,在點積注意力和 2-單純注意力中與相同數量的不同 KV 詞元進行互動,我們將 FA3 的 KV 序列長度設定為 W1 x W2,不帶因果掩碼。我們的基準測試結果顯示,FA3 實現了高達 750 TFLOPs,這表明我們最好的 2-單純注意力實現達到了 FA3 峰值效能的約 78.4%。
我們還測量了 TLX 版本 FlashAttention [10] 的峰值 TFLOPs,結果如下:
| FA TLX-WS 核心 | FA TLX-WS + 計算流水線核心 | FA TLX-WS + 計算流水線 + 乒乓核心 | |
| 峰值 TFLOPs | 590 | 680 | 717 |
我們的快速 2-單純 TLX-WS(核心 1)核心實現了與 FA TLX-WS 幾乎相同的峰值 TFLOPs。剩餘的效能差距主要源於計算流水線和乒乓最佳化尚未在 2-單純注意力核心中完全發揮作用,這是我們計劃在未來工作中解決的領域。
結論
在這篇部落格中,我們提出了一種設計硬體對齊的 2-單純注意力核心演算法的綜合方法,展示了系統最佳化如何實現強大效能。我們介紹了一種實現融合 2-單純注意力核心的簡潔演算法,並採用了 Hopper 的一些特性,例如用於標準點積注意力的 FlashAttention 2.X。
未來仍有幾個領域有待開發:啟用計算流水線、開發用於反向傳播和解碼形狀的快速核心、實現持久排程以及沿 N 維度劃分消費者組以支援小 GQA 比率。
我們希望這項工作能為尋求透過硬體對齊設計改進注意力機制的研究人員提供寶貴的見解!
致謝
我們衷心感謝 Vijay Krishnamoorthy、Jing Zhang、Yang Chen、Mark Saroufim 和 Bert Maher 對這篇部落格文章的審閱和寶貴反饋。我們還要感謝 Daohang Shi、Peng Chen 和 Manman Ren 在解決 TLX 相關問題上的幫助。
參考文獻
[1] 快速而簡潔:Triton 中的 2-單純注意力:https://arxiv.org/pdf/2507.02754
[2] TLX – Triton 低階擴充套件:https://github.com/facebookexperimental/triton/tree/tlx
[3] 邏輯與 2-單純 Transformer:https://arxiv.org/abs/1909.00668
[3] FlashAttention-2:https://arxiv.org/abs/2307.08691
[4] FlashAttention-3:https://arxiv.org/abs/2407.08608
[5] 原生稀疏注意力:https://arxiv.org/abs/2502.11089
[6] PTX WGMMA 矩陣形狀:https://docs.nvidia.com/cuda/parallel-thread-execution/#asynchronous-warpgroup-level-matrix-shape
[7] H100 SXM:https://resources.nvidia.com/en-us-gpu-resources/h100-datasheet-24306
- BF16 Tensor Core:989 TFlops
- BF16 Cuda Core:134 TFlops
- BF16 Tensor Core 與 Cuda Core 之比 = 7.38x
[8] Proton – Triton 分析器:https://github.com/triton-lang/triton/tree/main/third_party/proton
[9] 基準測試設定
- H100 SXM 功率設定:700W
- FlashAttention v2.8.3
- CUDA 12.6
附錄
[1] 2D SWA 浪費計算的計算
------------------------------ Parameters: M=64, KV=128, N=8192, W1=32, W2=512, D=128 Tiling Sequence: Efficiency: 26.80% Waste: 73.20% Tiling Heads: Efficiency: 98.65% Waste: 1.35%
[2] 2-單純注意力前向傳播的 Tensor Core TFLOPs 計算
[3] 點積和三線性積
def dot_product(A, B): """ Standard dot product (matrix multiplication) Input: A in [M, K], B in [N, K] Output: C in [M, N] This is equivalent to A @ B.T """ M, K = A.shape N, K2 = B.shape assert K == K2, "Inner dimensions must match" C = np.zeros((M, N)) for i in range(M): for j in range(N): C[i][j] = sum(A[i][inner_k] * B[j][inner_k] for inner_k in range(K)) return C def trilinear_product_2D_to_3D(A, B1, B2): """ Trilinear product for computing 3D attention logits Input: A in [M, K], B1 in [N, K], B2 in [N, K] Output: C in [M, N, N] Each element C[i,j,k] is the sum of element-wise products of A[i,:], B1[j,:], and B2[k,:] along the K dimension """ M, K = A.shape N, K1 = B1.shape N2, K2 = B2.shape assert K == K1 == K2, "All K dimensions must match" assert N == N2, "N dimensions must match" C = np.zeros((M, N, N)) for i in range(M): for j in range(N): for k in range(N): C[i][j][k] = sum(A[i][inner_k] * B1[j][inner_k] * B2[k][inner_k] for inner_k in range(K)) return C def trilinear_product_3D_to_2D(A, B1, B2): """ Trilinear product for aggregating with 3D attention weights Input: A in [M, N, N], B1 in [N, K], B2 in [N, K] Output: C in [M, K] Uses 3D attention weights A to aggregate information from B1 and B2 """ M, N, N2 = A.shape assert N == N2, "A must be square in last two dimensions" N3, K = B1.shape N4, K2 = B2.shape assert N == N3 == N4, "N dimensions must match" assert K == K2, "K dimensions must match" C = np.zeros((M, K)) for i in range(M): for k in range(K): C[i][k] = sum(A[i][a][b] * B1[a][k] * B2[b][k] for a in range(N) for b in range(N)) return C
[4] 演算法 3:前向 + Warp 專用化

[5] CUDA Core 計算的理論分析
為簡化分析,我們省略了批次維度 (B) 並採用以下符號:
- Hq:查詢頭數
- N:序列長度
- D:頭部維度
- Hkv:鍵值頭數 (= 1),在此計算中也省略
- BLOCK_M:查詢頭部的瓦片大小 (= Hq)
- BLOCK_KV:KV 序列長度維度的瓦片大小
Tensor Core TFLOPs
N × Hq × D × W1 × W2 × 2 × 2 = 4 × N × Hq × D × W1 × W2
CUDA Core TFLOPs(僅計算 2-單純注意力引入的 CUDA Core TFLOPs)
QK1 計算
- 每個 CTA:W1 × BLOCK_M × D
- CTA 數量:N
- 總計:N × W1 × BLOCK_M × D
PV2V1 計算
- 每個 CTA:W1 × (W2 / BLOCK_KV) × BLOCK_M × D
- CTA 數量:N
- 總計:N × W1 × (W2 / BLOCK_KV) × BLOCK_M × D
組合 CUDA Core TFLOPs
N × W1 × BLOCK_M × D + N × W1 × (W2 / BLOCK_KV) × BLOCK_M × D = N × W1 × BLOCK_M × D × (1 + W2 / BLOCK_KV)
比率分析
Tensor Core / CUDA Core = 4 × W2 × BLOCK_KV / (BLOCK_KV + W2)
例如,在 BLOCK_KV = 128 和 W2 = 512 的情況下,Tensor Core TFLOPs 大約超過 CUDA Core TFLOPs 410 倍,其中 Tensor Core 比 Cuda Core 快約 7.38 倍 [7]。因此,CUDA Core 計算 不會 成為 2-單純注意力核心的瓶頸。