參差張量運算子¶

高階概觀¶

參差張量運算子的目的是處理輸入資料的某些維度「參差不齊」的情況，亦即，給定維度中的每個連續列可能長度不同。這類似於 PyTorch 中的 NestedTensor 實作以及 Tensorflow 中的 RaggedTensor 實作。

此類型輸入的兩個著名範例為

推薦系統中的稀疏特徵輸入
可能輸入至自然語言處理系統的符號化句子批次。

參差張量格式¶

參差張量在 FBGEMM_GPU 中有效地表示為三個張量物件。這三個張量為：值、最大長度和 偏移量。

值¶

值 定義為一個 2D 張量，其中包含參差張量中的所有元素值，亦即 Values.numel() 是參差張量中元素的數量。值 中每一列的大小是從參差張量中最小（最內層）維度子張量（不包括大小為 0 的張量）的最大公約數衍生而來。

偏移量¶

偏移量 是一個張量清單，其中每個張量 Offsets[i] 代表清單中下一個張量 Offsets[i + 1] 值的分割索引。

例如，Offset[i] = [ 0, 3, 4 ] 表示目前維度 i 分為兩組，以索引邊界 [0 , 3) 和 [3, 4) 表示。對於每個 Offsets[i]，其中 0 <= i < len(Offests) - 1，Offsets[i][0] = 0，且 Offsets[i][-1] = Offsets[i+1].length。

Offsets[-1] 指的是 值 的外層維度索引（列索引），亦即 offsets[-1] 將會是 值 本身的分割索引。因此，Offsets[-1] 張量以 0 開頭，並以 Values.size(0)（亦即 值 的列數）結尾。

最大長度¶

最大長度 是一個整數清單，其中每個值 MaxLengths[i] 代表 Offsets[i] 中對應偏移量值之間的最大值

MaxLengths[i] = max( Offsets[i][j] - Offsets[i][j-1]  |  0 < j  < len(Offsets[i]) )

最大長度 中的資訊用於執行從參差張量到將用於判斷張量密集形式形狀的標準（密集）張量的轉換。

參差張量範例¶

下圖顯示一個範例參差張量，其中包含三個 2D 子張量，每個子張量都有不同的維度

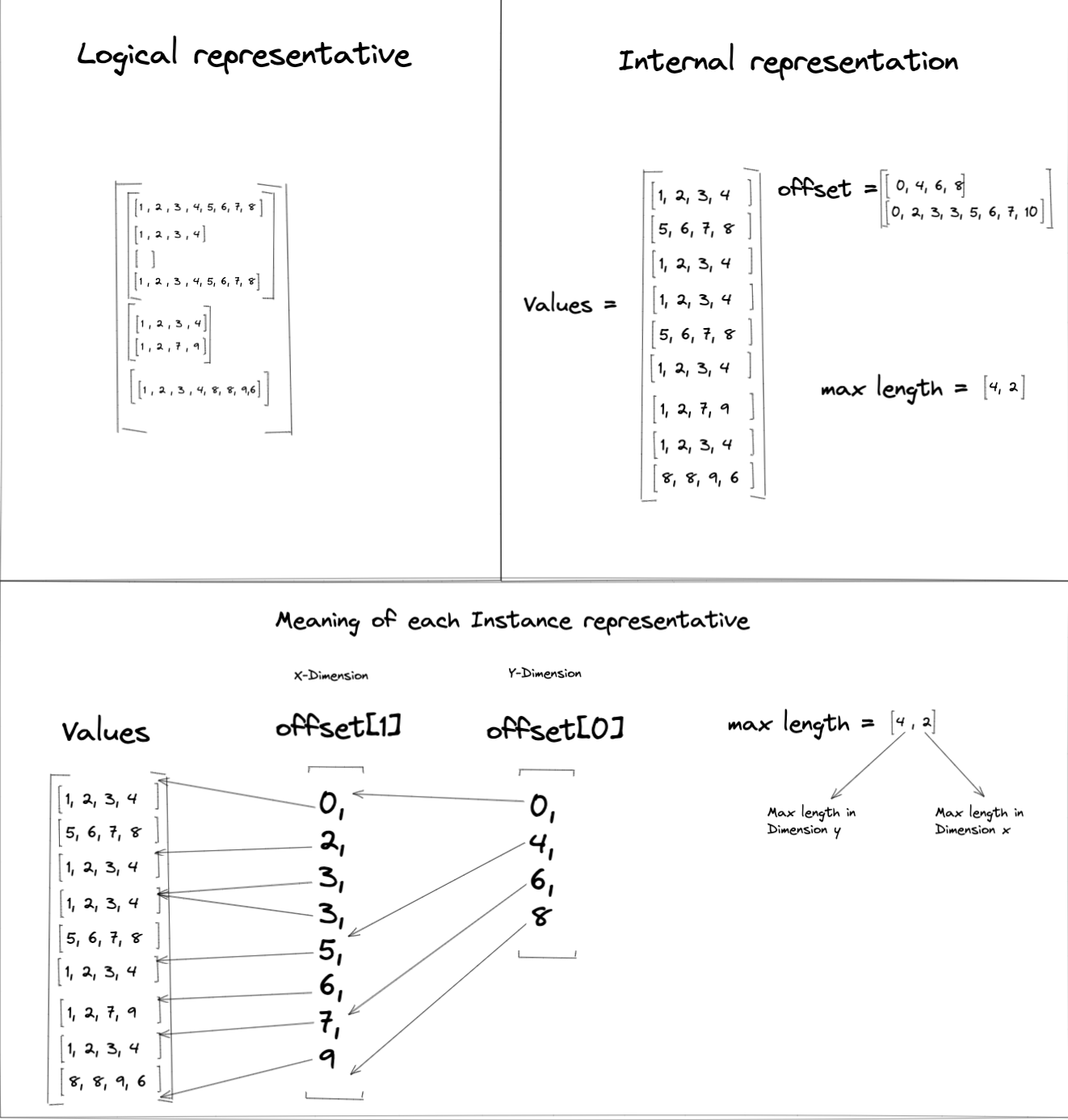
在此範例中，參差張量最內層維度中列的大小為 8、4 和 0，因此 值 中每列的元素數量設定為 4（最大公約數）。這表示 值 的大小必須為 9 x 4，才能容納參差張量中的所有值。

由於範例參差張量包含 2D 子張量，因此 偏移量 清單需要長度為 2，才能建立分割索引。Offsets[0] 代表維度 0 的分割，而 Offsets[1] 代表維度 1 的分割。

範例參差張量中的 最大長度 值為 [4 , 2]。MaxLengths[0] 是從 Offsets[0] 範圍 [4, 0) 衍生而來，而 MaxLengths[1] 則是從 Offsets[1] 範圍 [0, 2)（或 [7, 9]、[3,5]）衍生而來。

以下表格列出套用至 值 張量的分割索引，以建構範例參差張量的邏輯表示法

`Offsets[0]`	`Offsets[0]` 範圍	`Offsets[0]` 群組	對應的 `Offsets[1]`	`Offsets[1]` 範圍	`值` 群組	對應的 `值`
`[ 0, 4, 6, 8 ]`	`[0, 4)`	群組 1	`[ 0, 2, 3, 3, 5 ]`	`[ 0, 2 )`	群組 1	`[ [ 1, 2, 3, 4 ], [ 5, 6, 7, 8 ] ]`
				`[ 2, 3 )`	群組 2	`[ [ 1, 2, 3, 4 ] ]`
				`[ 3, 3 )`	群組 3	`[ ]`
				`[ 3, 5 )`	群組 4	`[ [ 1, 2, 3, 4 ], [ 5, 6, 7, 8 ] ]`
	`[4, 6)`	群組 2	`[ 5, 6, 7 ]`	`[ 5, 6 )`	群組 5	`[ [ 1, 2, 3, 4 ] ]`
				`[ 6, 7 )`	群組 6	`[ [ 1, 2, 7, 9 ] ]`
	`[6, 8)`	群組 3	`[ 7, 9 ]`	`[ 7, 9 )`	群組 7	`[ [ 1, 2, 3, 4 ], [ 8, 8, 9, 6 ] ]`

參差張量運算¶

在目前階段，FBGEMM_GPU 僅支援參差張量的元素級加法、乘法和轉換運算。

算術運算¶

參差張量加法和乘法的工作方式與阿達瑪乘積類似，且僅涉及參差張量的 值。例如

\[\begin{split}\begin{bmatrix} \begin{bmatrix} 1. & 2. \\ 3. & 4. \\ \end{bmatrix} \\ \begin{bmatrix} 5. & 6. \\ \end{bmatrix} \\ \begin{bmatrix} 7. & 8. \\ 9. & 10. \\ 11. & 12. \\ \end{bmatrix} \\ \end{bmatrix} \times \begin{bmatrix} \begin{bmatrix} 1. & 2. \\ 3. & 4. \\ \end{bmatrix} \\ \begin{bmatrix} 5. & 6. \\ \end{bmatrix} \\ \begin{bmatrix} 7. & 8. \\ 9. & 5. \\ 2. & 3. \\ \end{bmatrix} \\ \end{bmatrix} \rightarrow \begin{bmatrix} \begin{bmatrix} 1. & 4. \\ 9. & 16. \\ \end{bmatrix} \\ \begin{bmatrix} 25. & 36. \\ \end{bmatrix} \\ \begin{bmatrix} 49. & 64. \\ 81. & 50. \\ 22. & 36. \\ \end{bmatrix} \\ \end{bmatrix}\end{split}\]

因此，參差張量的算術運算要求兩個運算元具有相同的形狀。換句話說，如果我們有參差張量 \(A\)、\(X\)、\(B\) 和 \(C\)，其中 \(C = AX + B\)，則下列屬性成立

// MaxLengths are the same
C.maxlengths == A.maxlengths == X.maxlengths == B.maxlengths

// Offsets are the same
C.offsets == A.offsets == X.offsets == B.offsets

// Values are elementwise equal to the operations applied
C.values[i][j] == A.values[i][j] * X.values[i][j] + B.values[i][j]

轉換運算¶

參差轉密集¶

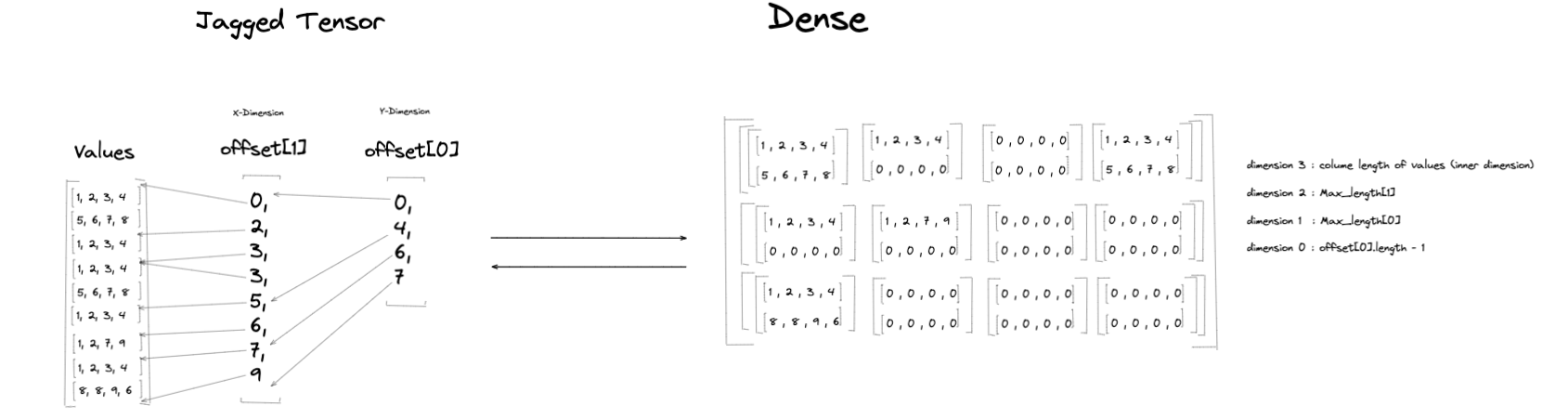
../../_images/JaggedTensorConversion1.png

將參差張量 \(J\) 轉換為等效密集張量 \(D\) 是從空的密集張量開始。\(D\) 的形狀基於 最大長度、值 的內層維度，以及 Offsets[0] 的長度。\(D\) 中的維度數為

rank(D) = len(MaxLengths) + 2

對於 \(D\) 中的每個維度，維度大小為

dim(i) = MaxLengths[i-1]  // (0 < i < D.rank-1)

使用來自參差張量範例的範例參差張量，len(MaxLengths) = 2，因此等效密集張量的秩（維度數）將為 4。範例參差張量有兩個偏移量張量，Offsets[0] 和 Offsets[1]。在轉換過程中，元素將根據 Offsets[0] 和 Offsets[1] 的分割索引中表示的範圍，從 值 載入到密集張量上（請參閱表格，以了解群組到密集表格中對應列的對應）

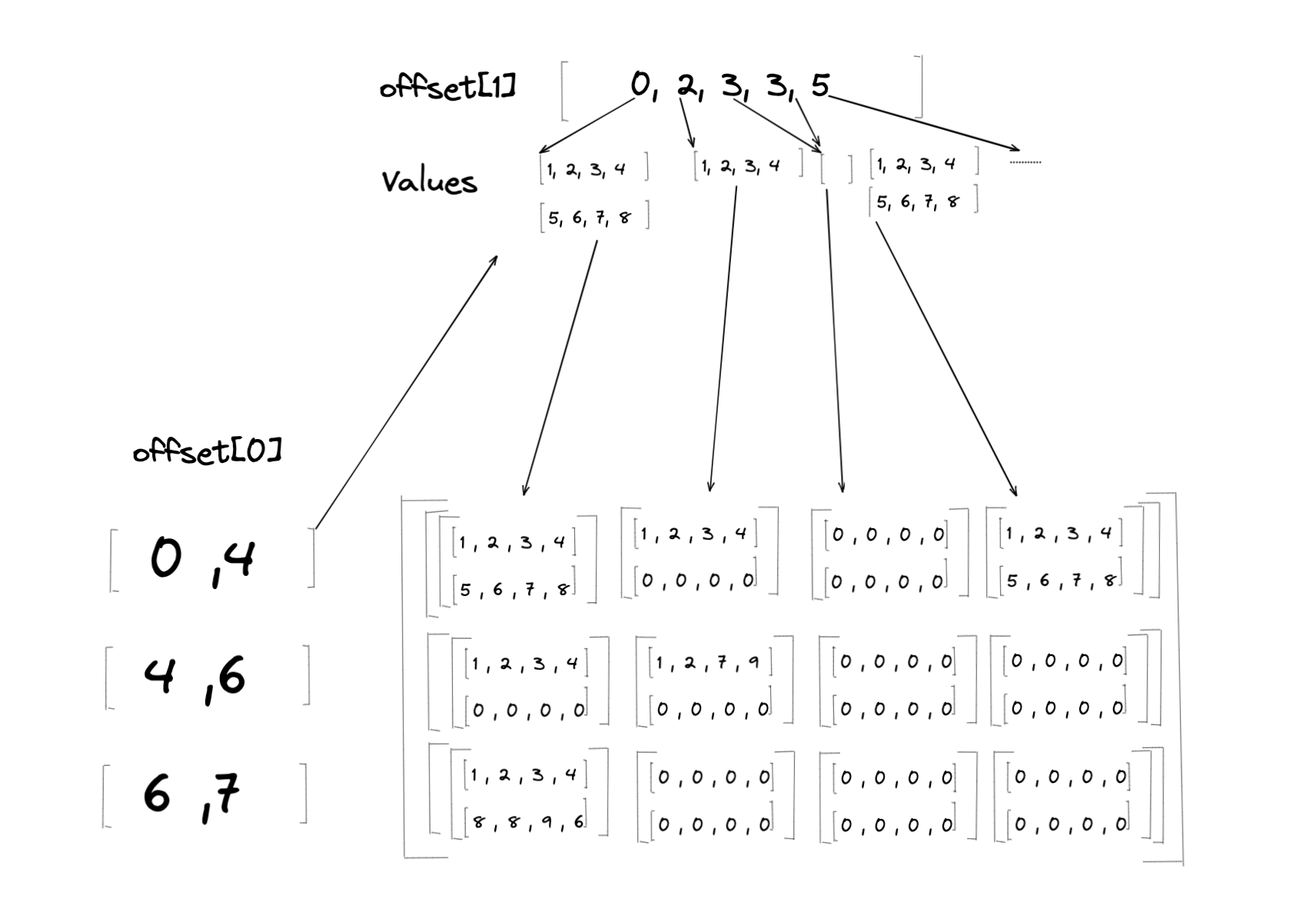
../../_images/JaggedTensorConversion2.png

由於並非 Offsets[i] 中表示的每個分割範圍的大小都等於 MaxLengths[i]，因此 \(D\) 的某些部分不會從 \(J\) 載入值。在這種情況下，這些部分將以填充值進行填充。在上述範例中，填充值為 0。

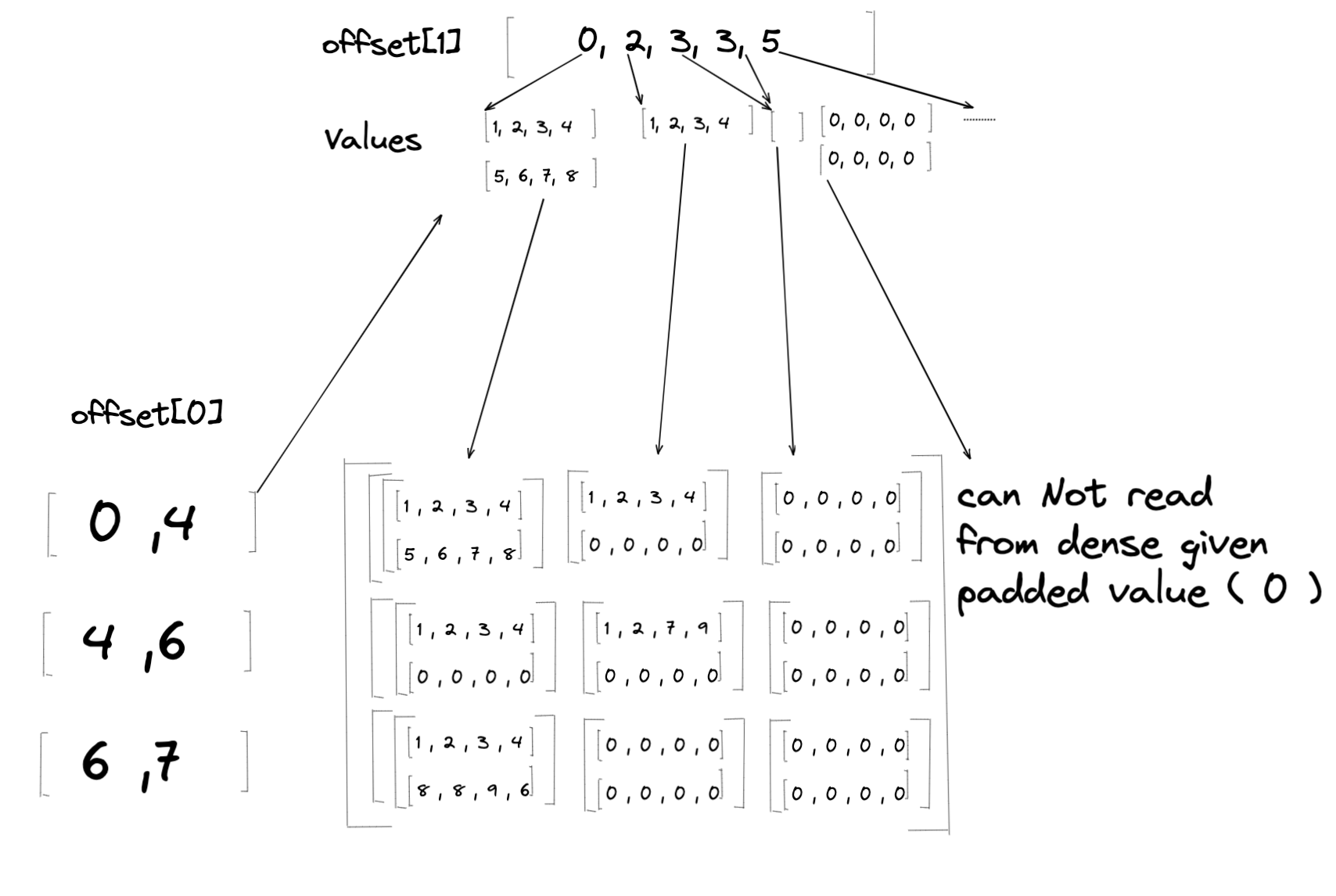
密集轉參差¶

對於從密集張量到參差張量的轉換，密集張量中的值會載入到參差張量的 值 中。但是，給定的密集張量可能與參照 偏移量 的形狀不同。如果密集的相關維度小於預期，則可能導致參差張量無法讀取相應密集位置的情況。當這種情況發生時，我們會將填充值提供給對應的 值（請參閱下文）

../../_images/JaggedTensorConversion3.png

合併算術 + 轉換運算¶

在某些情況下，我們會想要執行下列運算

dense_tensor + jagged_tensor → dense_tensor (or jagged_tensor)

我們可以將此類運算分解為兩個步驟

轉換運算 - 根據目標張量的所需格式，從參差 → 密集或密集 → 參差轉換。轉換後，運算元張量（無論是密集還是參差）應具有完全相同的形狀。
算術運算 - 針對密集或參差張量照常執行算術運算。