不規則張量運算子

高層概述

不規則張量運算子的目的是處理輸入資料的某個維度是“不規則的”情況，即給定維度中的連續行可能具有不同的長度。這類似於 PyTorch 中的 NestedTensor 實現 和 Tensorflow 中的 RaggedTensor 實現。

這種輸入的兩個顯著示例是

• 推薦系統中的稀疏特徵輸入

• 可能輸入到自然語言處理系統的批處理標記化句子。

不規則張量格式

不規則張量在 FBGEMM_GPU 中實際上表示為三張量物件。這三個張量是：**Values**（值）、**MaxLengths**（最大長度）和 **Offsets**（偏移量）。

Values（值）

Values 定義為一個 2D 張量，其中包含不規則張量中的所有元素值，即 Values.numel() 是不規則張量中的元素數量。Values 中每一行的大小由不規則張量中最小（最內層）維子張量（不包含大小為 0 的張量）的最大公約數確定。

Offsets（偏移量）

Offsets 是一個張量列表，其中每個張量 Offsets[i] 表示列表中下一個張量 Offsets[i + 1] 的值的分割槽索引。

例如，Offset[i] = [ 0, 3, 4 ] 意味著當前維度 i 被分成兩組，由索引邊界 [0 , 3) 和 [3, 4) 表示。對於每個 Offsets[i]（其中 0 <= i < len(Offsets) - 1），Offsets[i][0] = 0，且 Offsets[i][-1] = Offsets[i+1].length。

Offsets[-1] 指的是 Values 的外層維度索引（行索引），即 offsets[-1] 將是 Values 本身的分割槽索引。因此，Offsets[-1] 張量以 0 開始，以 Values.size(0) 結束（即 Values 的行數）。

Max Lengths（最大長度）

MaxLengths 是一個整數列表，其中每個值 MaxLengths[i] 表示 Offsets[i] 中對應偏移量值之間的最大值。

MaxLengths[i] = max( Offsets[i][j] - Offsets[i][j-1]  |  0 < j  < len(Offsets[i]) )

MaxLengths 中的資訊用於執行從不規則張量到普通（密集）張量的轉換，其中它將用於確定張量密集形式的形狀。

不規則張量示例

下圖顯示了一個不規則張量示例，其中包含三個 2D 子張量，每個子張量具有不同的維度

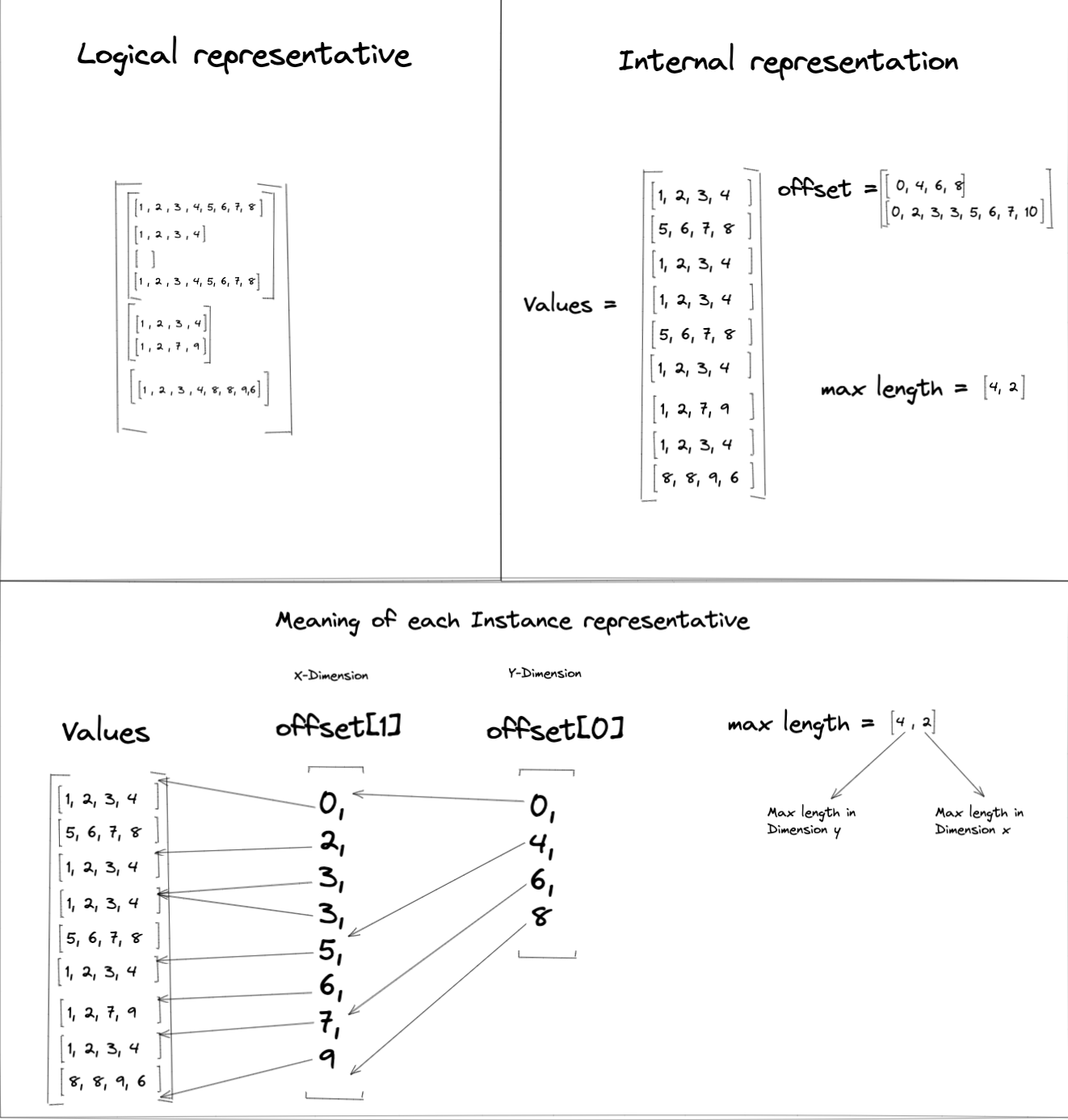
在此示例中，不規則張量最內層維度中行的大小分別為 8、4 和 0，因此 Values 中每行的元素數量設定為 4（最大公約數）。這意味著 Values 必須具有 9 x 4 的大小，以便容納不規則張量中的所有值。

因為示例不規則張量包含 2D 子張量，所以 Offsets 列表需要具有長度 2 來建立分割槽索引。Offsets[0] 表示維度 0 的分割槽，Offsets[1] 表示維度 1 的分割槽。

示例不規則張量中的 MaxLengths 值是 [4 , 2]。MaxLengths[0] 由 Offsets[0] 範圍 [4, 0) 得出，MaxLengths[1] 由 Offsets[1] 範圍 [0, 2)（或 [7, 9]、[3,5]）得出。

下表顯示了應用於 Values 張量以構建示例不規則張量邏輯表示的分割槽索引。

Offsets[0]	Offsets[0] 範圍	Offsets[0] 組	對應的 Offsets[1]	Offsets[1] 範圍	Values 組	對應的 Values
[ 0, 4, 6, 8 ]	[0, 4)	第 1 組	[ 0, 2, 3, 3, 5 ]	[ 0, 2 )	第 1 組	[ [ 1, 2, 3, 4 ], [ 5, 6, 7, 8 ] ]
				[ 2, 3 )	第 2 組	[ [ 1, 2, 3, 4 ] ]
				[ 3, 3 )	第 3 組	[ ]
				[ 3, 5 )	第 4 組	[ [ 1, 2, 3, 4 ], [ 5, 6, 7, 8 ] ]
	[4, 6)	第 2 組	[ 5, 6, 7 ]	[ 5, 6 )	第 5 組	[ [ 1, 2, 3, 4 ] ]
				[ 6, 7 )	第 6 組	[ [ 1, 2, 7, 9 ] ]
	[6, 8)	第 3 組	[ 7, 9 ]	[ 7, 9 )	第 7 組	[ [ 1, 2, 3, 4 ], [ 8, 8, 9, 6 ] ]

不規則張量操作

在當前階段，FBGEMM_GPU 僅支援不規則張量的元素級加法、乘法和轉換操作。

算術操作

不規則張量加法和乘法類似於 Hadamard 乘積，且僅涉及不規則張量的 Values。例如

\[\begin{split}\begin{bmatrix} \begin{bmatrix} 1. & 2. \\ 3. & 4. \\ \end{bmatrix} \\ \begin{bmatrix} 5. & 6. \\ \end{bmatrix} \\ \begin{bmatrix} 7. & 8. \\ 9. & 10. \\ 11. & 12. \\ \end{bmatrix} \\ \end{bmatrix} \times \begin{bmatrix} \begin{bmatrix} 1. & 2. \\ 3. & 4. \\ \end{bmatrix} \\ \begin{bmatrix} 5. & 6. \\ \end{bmatrix} \\ \begin{bmatrix} 7. & 8. \\ 9. & 5. \\ 2. & 3. \\ \end{bmatrix} \\ \end{bmatrix} \rightarrow \begin{bmatrix} \begin{bmatrix} 1. & 4. \\ 9. & 16. \\ \end{bmatrix} \\ \begin{bmatrix} 25. & 36. \\ \end{bmatrix} \\ \begin{bmatrix} 49. & 64. \\ 81. & 50. \\ 22. & 36. \\ \end{bmatrix} \\ \end{bmatrix}\end{split}\]

因此，不規則張量的算術操作要求兩個運算元具有相同的形狀。換句話說，如果我們有不規則張量 \(A\)、\(X\)、\(B\) 和 \(C\)，其中 \(C = AX + B\)，則以下屬性成立：

// MaxLengths are the same
C.maxlengths == A.maxlengths == X.maxlengths == B.maxlengths

// Offsets are the same
C.offsets == A.offsets == X.offsets == B.offsets

// Values are elementwise equal to the operations applied
C.values[i][j] == A.values[i][j] * X.values[i][j] + B.values[i][j]

轉換操作

不規則到密集

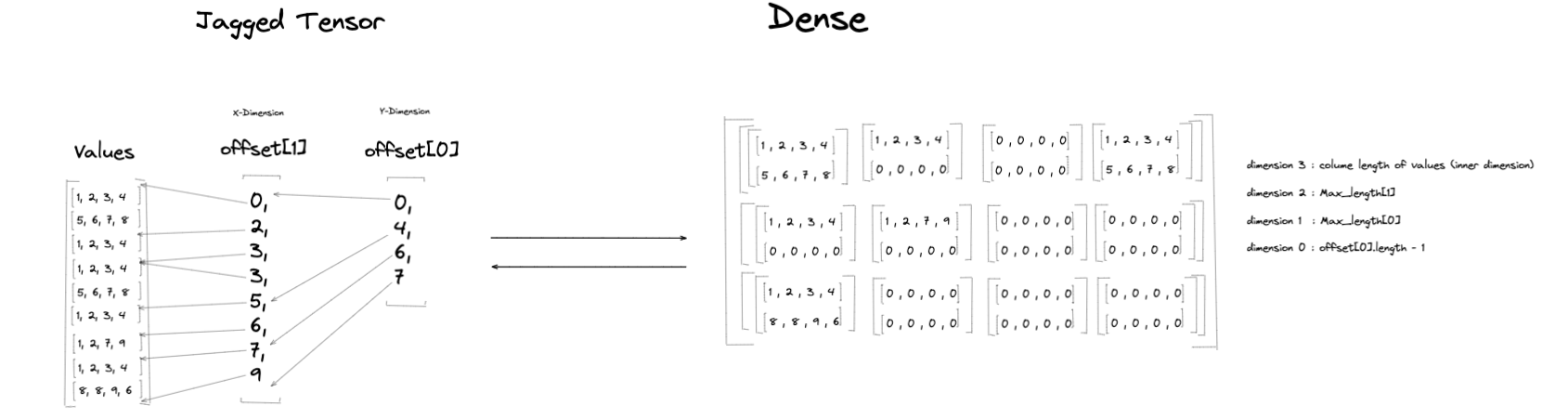
將不規則張量 \(J\) 轉換為等效的密集張量 \(D\) 從一個空的密集張量開始。\(D\) 的形狀基於 MaxLengths、Values 的內層維度和 Offsets[0] 的長度。\(D\) 的維度數是

rank(D) = len(MaxLengths) + 2

對於 \(D\) 中的每個維度，維度大小是

dim(i) = MaxLengths[i-1]  // (0 < i < D.rank-1)

使用 不規則張量示例 中的示例不規則張量，len(MaxLengths) = 2，因此等效密集張量的秩（維度數）將是 4。示例不規則張量有兩個偏移量張量，Offsets[0] 和 Offsets[1]。在轉換過程中，Values 中的元素將根據 Offsets[0] 和 Offsets[1] 的分割槽索引中所示的範圍載入到密集張量上（參見表瞭解組與密集表中的對應行的對映）。

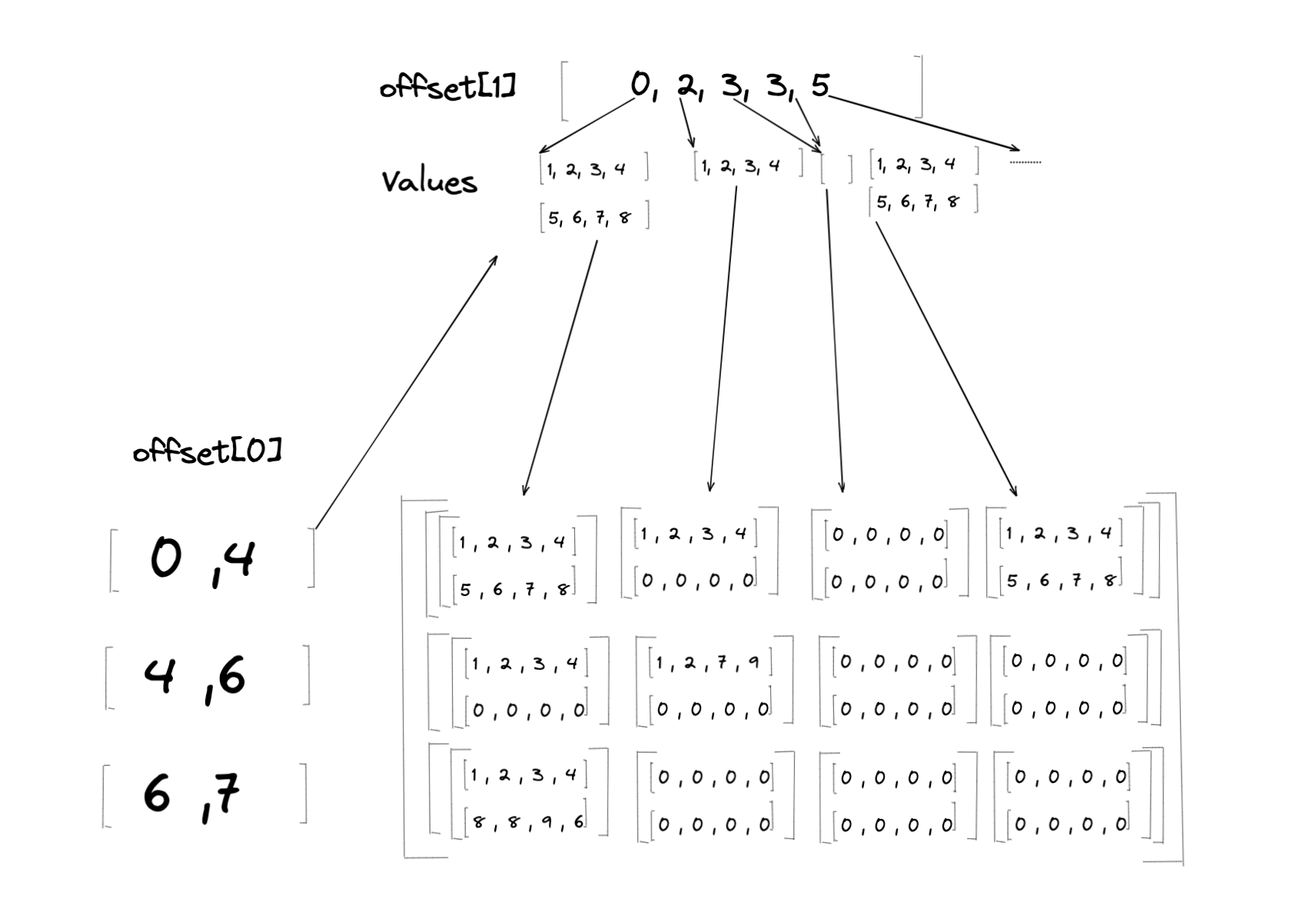
\(D\) 的某些部分不會載入來自 \(J\) 的值，因為 Offsets[i] 中所示的並非每個分割槽範圍的大小都等於 MaxLengths[i]。在這種情況下，這些部分將用一個填充值進行填充。在上述示例中，填充值是 0。

密集到不規則

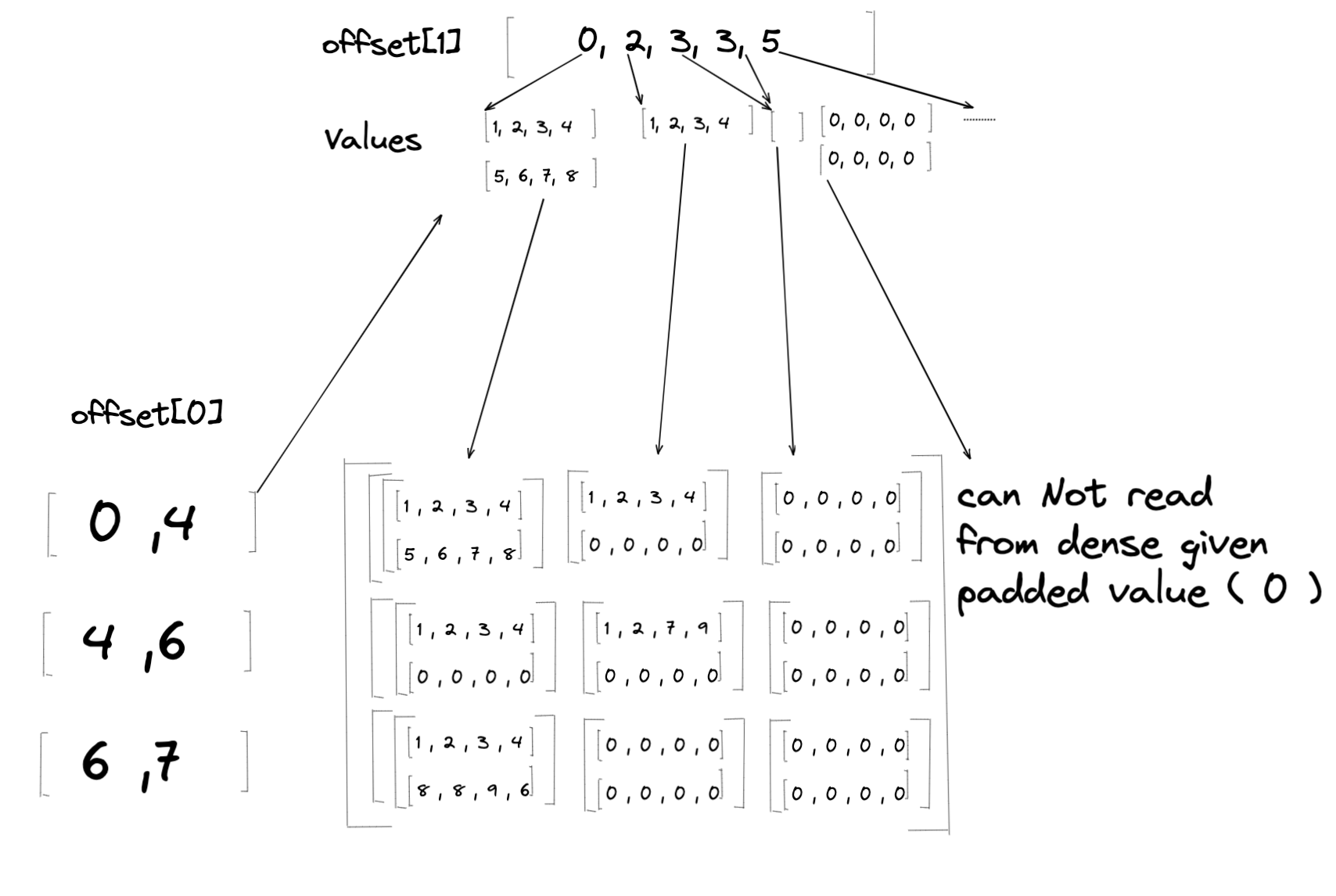
對於從密集張量到不規則張量的轉換，密集張量中的值被載入到不規則張量的 Values 中。然而，給定的密集張量可能與 Offsets 參考的形狀不同。如果密集張量的相關維度小於預期，這可能導致不規則張量無法讀取相應的密集位置。發生這種情況時，我們將填充值賦給對應的 Values（見下文）。

組合算術 + 轉換操作

在某些情況下，我們希望執行以下操作

dense_tensor + jagged_tensor → dense_tensor (or jagged_tensor)

我們可以將此類操作分解為兩個步驟

1. 轉換操作 - 根據目標張量的所需格式，從不規則轉換為密集，或從密集轉換為不規則。轉換後，運算元張量（無論是密集還是不規則）應具有完全相同的形狀。

2. 算術操作 - 照常執行密集或不規則張量的算術操作。