濾波器設計教程

作者: Moto Hira

本教程展示瞭如何建立基本的數字濾波器（脈衝響應）及其屬性。

我們將探討基於窗函式-sinc 核的低通、高通和帶通濾波器，以及頻率取樣法。

警告

本教程需要原型 DSP 功能，這些功能在夜間構建版本中提供。

請參閱 https://pytorch.com.tw/get-started/locally 獲取安裝夜間構建版本的說明。

import torch
import torchaudio

print(torch.__version__)
print(torchaudio.__version__)

import matplotlib.pyplot as plt

2.7.0
2.7.0

from torchaudio.prototype.functional import frequency_impulse_response, sinc_impulse_response

窗函式-Sinc 濾波器

Sinc 濾波器是一種理想化的濾波器，它可以在不影響較低頻率的情況下移除截止頻率以上的頻率。

Sinc 濾波器在解析解中具有無限的濾波器寬度。在數值計算中，sinc 濾波器無法精確表達，因此需要進行近似。

窗函式-sinc 有限脈衝響應是對 sinc 濾波器的近似。它透過以下步驟獲得：首先計算給定截止頻率的 sinc 函式，然後截斷濾波器裙帶，並應用窗函式（例如 Hamming 窗）來減少截斷引入的偽影。

sinc_impulse_response() 根據給定的截止頻率生成窗函式-sinc 脈衝響應。

低通濾波器

脈衝響應

建立 sinc IR 就像將截止頻率值傳遞給 sinc_impulse_response() 一樣簡單。

cutoff = torch.linspace(0.0, 1.0, 9)
irs = sinc_impulse_response(cutoff, window_size=513)

print("Cutoff shape:", cutoff.shape)
print("Impulse response shape:", irs.shape)

Cutoff shape: torch.Size([9])
Impulse response shape: torch.Size([9, 513])

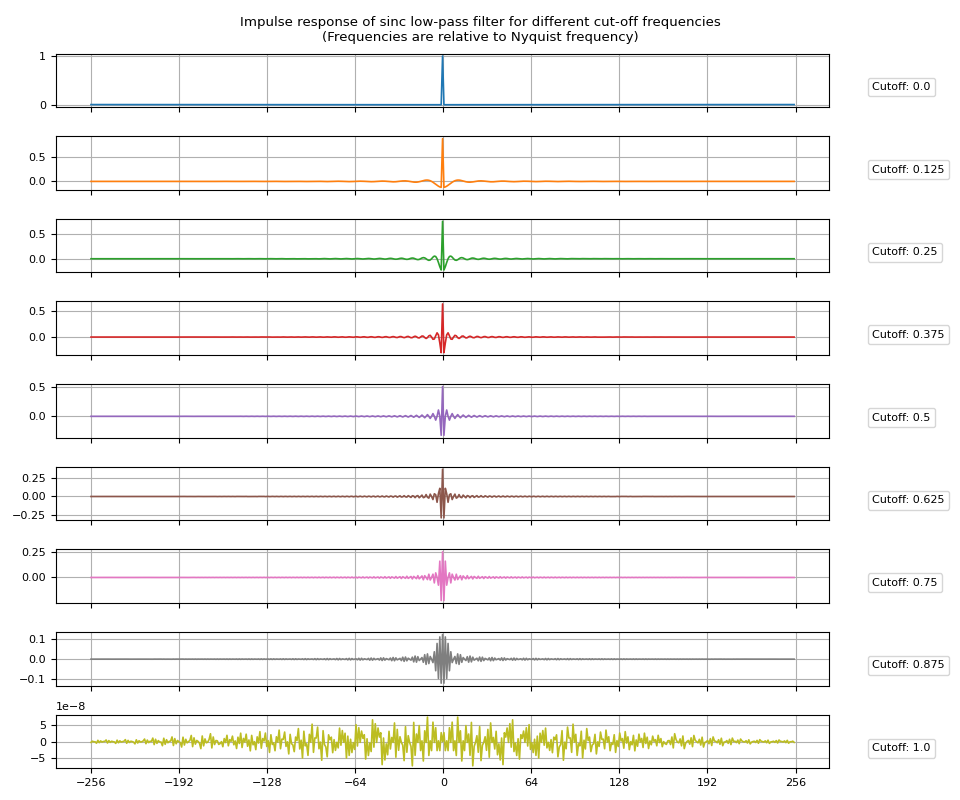
讓我們視覺化得到的脈衝響應。

def plot_sinc_ir(irs, cutoff):
    num_filts, window_size = irs.shape
    half = window_size // 2

    fig, axes = plt.subplots(num_filts, 1, sharex=True, figsize=(9.6, 8))
    t = torch.linspace(-half, half - 1, window_size)
    for ax, ir, coff, color in zip(axes, irs, cutoff, plt.cm.tab10.colors):
        ax.plot(t, ir, linewidth=1.2, color=color, zorder=4, label=f"Cutoff: {coff}")
        ax.legend(loc=(1.05, 0.2), handletextpad=0, handlelength=0)
        ax.grid(True)
    fig.suptitle(
        "Impulse response of sinc low-pass filter for different cut-off frequencies\n"
        "(Frequencies are relative to Nyquist frequency)"
    )
    axes[-1].set_xticks([i * half // 4 for i in range(-4, 5)])
    fig.tight_layout()

plot_sinc_ir(irs, cutoff)

頻率響應

接下來，讓我們看看頻率響應。簡單地對脈衝響應應用傅立葉變換即可得到頻率響應。

frs = torch.fft.rfft(irs, n=2048, dim=1).abs()

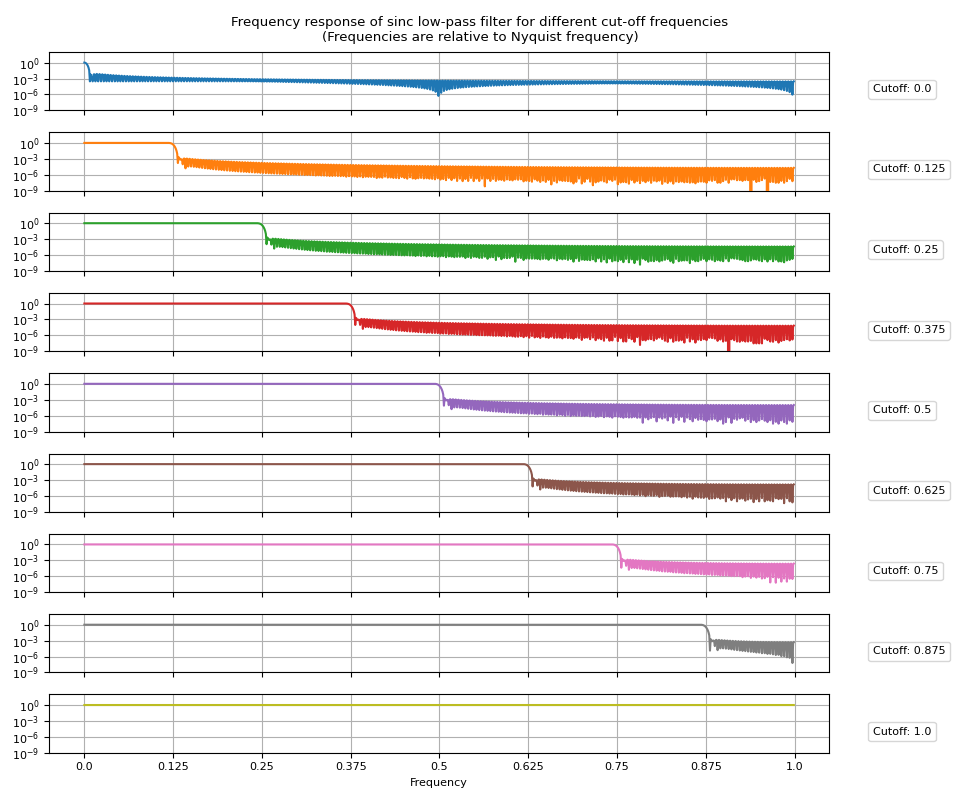
讓我們視覺化得到的頻率響應。

def plot_sinc_fr(frs, cutoff, band=False):
    num_filts, num_fft = frs.shape
    num_ticks = num_filts + 1 if band else num_filts

    fig, axes = plt.subplots(num_filts, 1, sharex=True, sharey=True, figsize=(9.6, 8))
    for ax, fr, coff, color in zip(axes, frs, cutoff, plt.cm.tab10.colors):
        ax.grid(True)
        ax.semilogy(fr, color=color, zorder=4, label=f"Cutoff: {coff}")
        ax.legend(loc=(1.05, 0.2), handletextpad=0, handlelength=0).set_zorder(3)
    axes[-1].set(
        ylim=[None, 100],
        yticks=[1e-9, 1e-6, 1e-3, 1],
        xticks=torch.linspace(0, num_fft, num_ticks),
        xticklabels=[f"{i/(num_ticks - 1)}" for i in range(num_ticks)],
        xlabel="Frequency",
    )
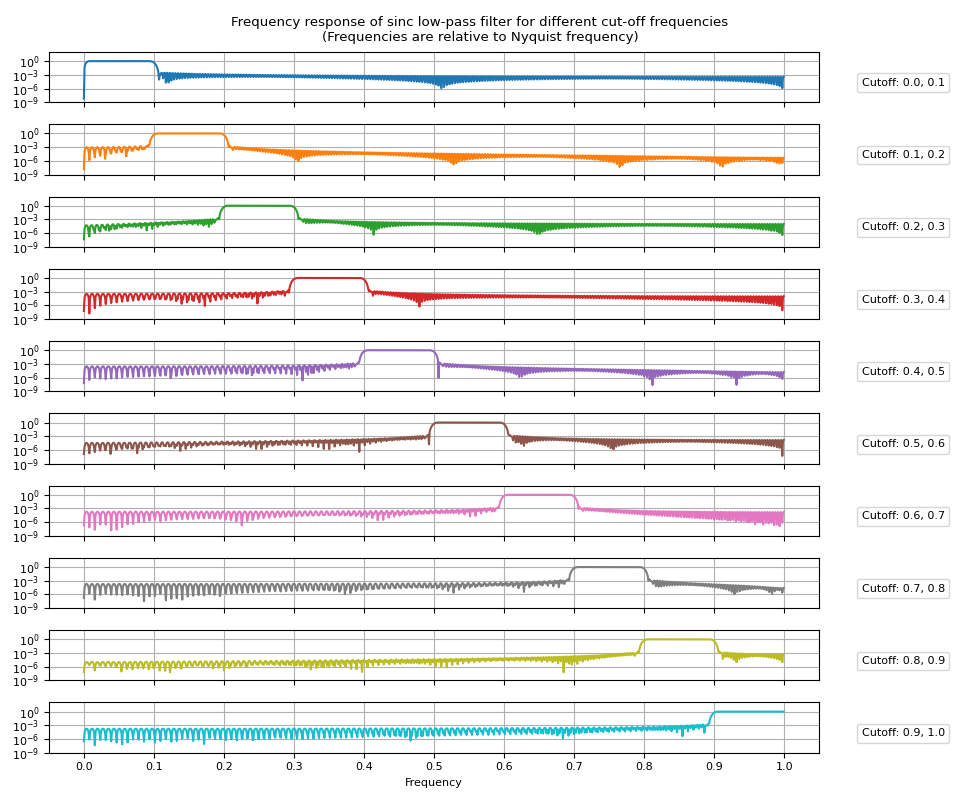
    fig.suptitle(
        "Frequency response of sinc low-pass filter for different cut-off frequencies\n"
        "(Frequencies are relative to Nyquist frequency)"
    )
    fig.tight_layout()

plot_sinc_fr(frs, cutoff)

高通濾波器

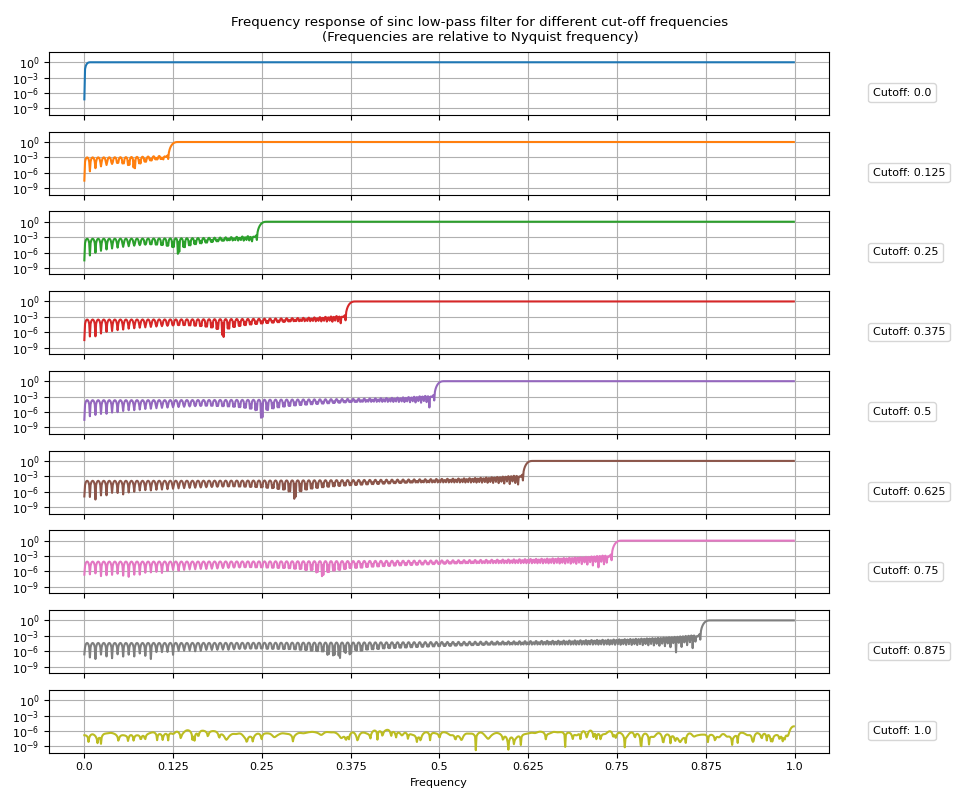
高通濾波器可以透過從 Dirac delta 函式中減去低通脈衝響應來獲得。

將 high_pass=True 傳遞給 sinc_impulse_response() 會將返回的濾波器核更改為高通濾波器。

irs = sinc_impulse_response(cutoff, window_size=513, high_pass=True)
frs = torch.fft.rfft(irs, n=2048, dim=1).abs()

脈衝響應

plot_sinc_ir(irs, cutoff)

頻率響應

plot_sinc_fr(frs, cutoff)

帶通濾波器

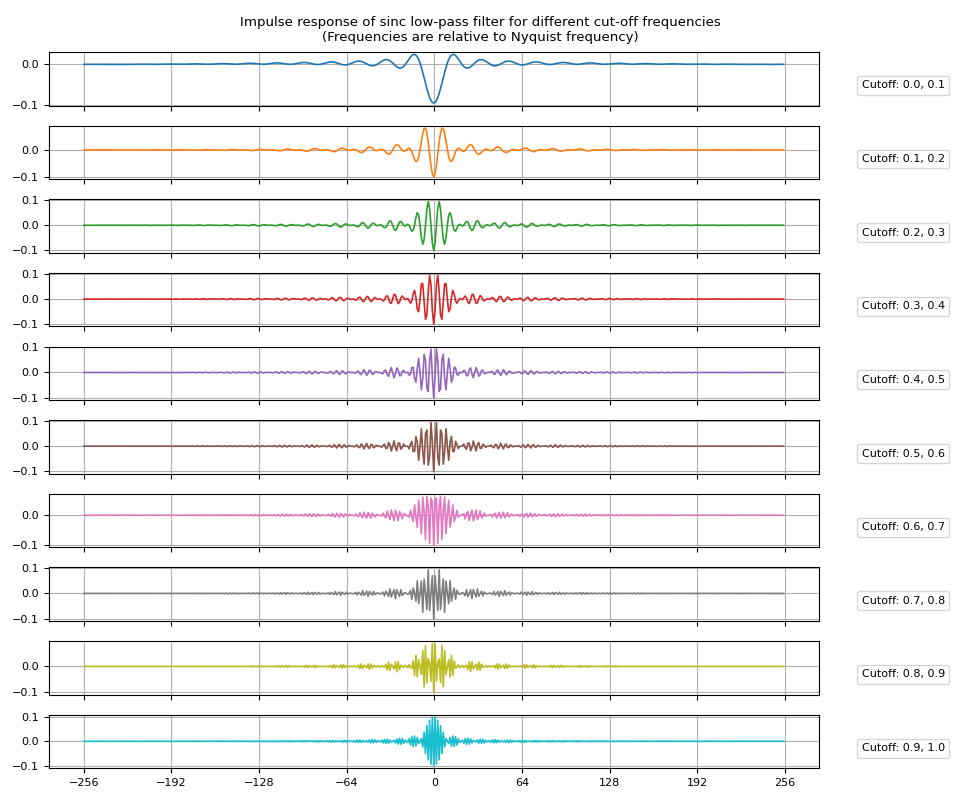
帶通濾波器可以透過從較低頻帶的低通濾波器中減去較高頻帶的低通濾波器來獲得。

cutoff = torch.linspace(0.0, 1, 11)
c_low = cutoff[:-1]
c_high = cutoff[1:]

irs = sinc_impulse_response(c_low, window_size=513) - sinc_impulse_response(c_high, window_size=513)
frs = torch.fft.rfft(irs, n=2048, dim=1).abs()

脈衝響應

coff = [f"{l.item():.1f}, {h.item():.1f}" for l, h in zip(c_low, c_high)]
plot_sinc_ir(irs, coff)

頻率響應

plot_sinc_fr(frs, coff, band=True)

頻率取樣

我們要研究的下一個方法從期望的頻率響應開始，透過應用逆傅立葉變換獲得脈衝響應。

frequency_impulse_response() 接收頻率的（未歸一化）幅度分佈，並從中構建脈衝響應。

但請注意，生成的脈衝響應並不會產生期望的頻率響應。

在下文中，我們將建立多個濾波器，並比較輸入的頻率響應和實際的頻率響應。

磚牆濾波器

讓我們從磚牆濾波器開始

magnitudes = torch.concat([torch.ones((128,)), torch.zeros((128,))])
ir = frequency_impulse_response(magnitudes)

print("Magnitudes:", magnitudes.shape)
print("Impulse Response:", ir.shape)

Magnitudes: torch.Size([256])
Impulse Response: torch.Size([510])

def plot_ir(magnitudes, ir, num_fft=2048):
    fr = torch.fft.rfft(ir, n=num_fft, dim=0).abs()
    ir_size = ir.size(-1)
    half = ir_size // 2

    fig, axes = plt.subplots(3, 1)
    t = torch.linspace(-half, half - 1, ir_size)
    axes[0].plot(t, ir)
    axes[0].grid(True)
    axes[0].set(title="Impulse Response")
    axes[0].set_xticks([i * half // 4 for i in range(-4, 5)])
    t = torch.linspace(0, 1, fr.numel())
    axes[1].plot(t, fr, label="Actual")
    axes[2].semilogy(t, fr, label="Actual")
    t = torch.linspace(0, 1, magnitudes.numel())
    for i in range(1, 3):
        axes[i].plot(t, magnitudes, label="Desired (input)", linewidth=1.1, linestyle="--")
        axes[i].grid(True)
    axes[1].set(title="Frequency Response")
    axes[2].set(title="Frequency Response (log-scale)", xlabel="Frequency")
    axes[2].legend(loc="center right")
    fig.tight_layout()

plot_ir(magnitudes, ir)

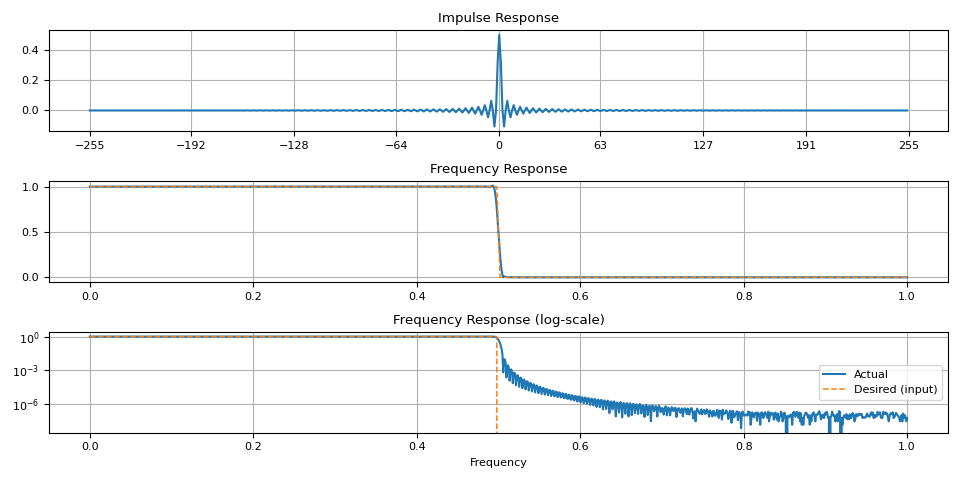
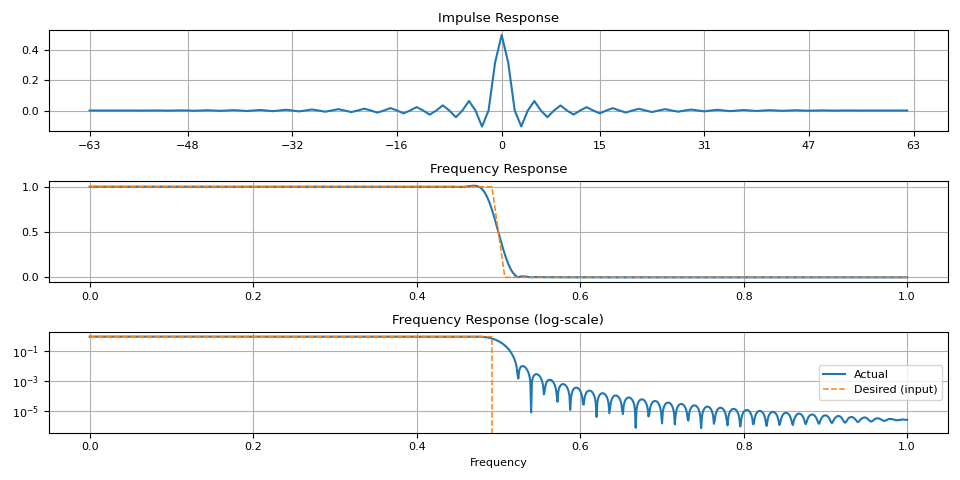
請注意，過渡帶附近存在偽影。當視窗大小較小時，這一點更加明顯。

magnitudes = torch.concat([torch.ones((32,)), torch.zeros((32,))])
ir = frequency_impulse_response(magnitudes)

plot_ir(magnitudes, ir)

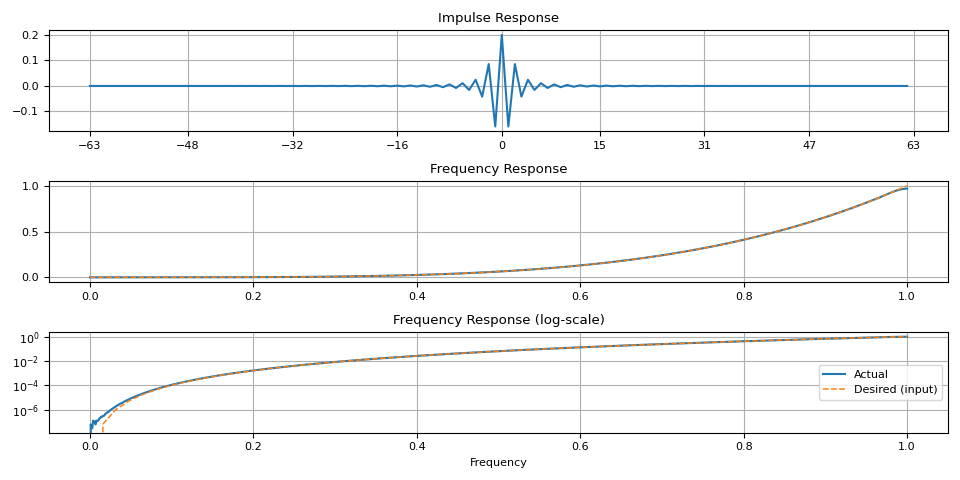
任意形狀

magnitudes = torch.linspace(0, 1, 64) ** 4.0
ir = frequency_impulse_response(magnitudes)

plot_ir(magnitudes, ir)

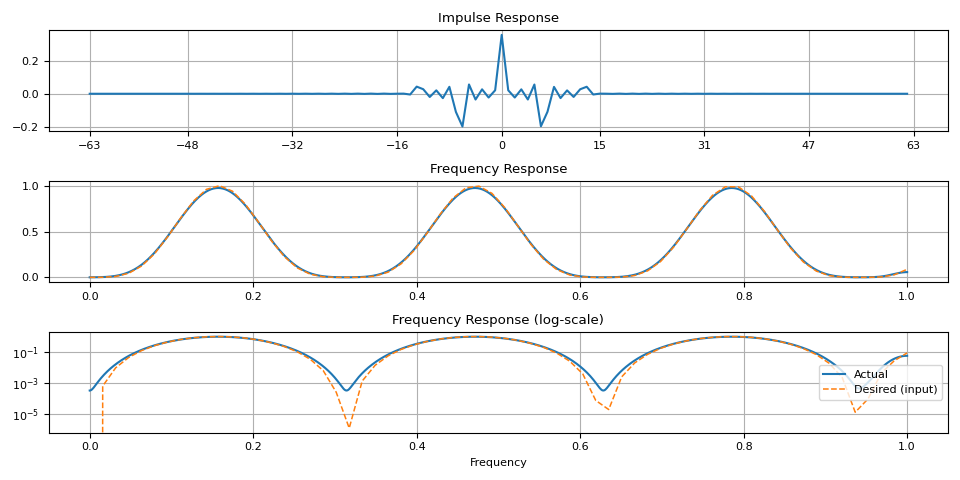
magnitudes = torch.sin(torch.linspace(0, 10, 64)) ** 4.0
ir = frequency_impulse_response(magnitudes)

plot_ir(magnitudes, ir)

參考文獻

• https://en.wikipedia.org/wiki/Sinc_filter

• https://www.analog.com/media/en/technical-documentation/dsp-book/dsp_book_Ch16.pdf

• https://courses.engr.illinois.edu/ece401/fa2020/slides/lec10.pdf

• https://ccrma.stanford.edu/~jos/sasp/Windowing_Desired_Impulse_Response.html